Home »
Data Structure
Creating minimum spanning tree from Prim's algorithm
In this article, we will learn about spanning tree, minimum spanning tree and how to create a minimum spanning tree from Prim’s algorithm?
By Manu Jemini, on January 09, 2018
What is Spanning Tree?
Spanning Tree is a subset of a graph, without any cycle. What this means is that if you can reach to node from a path A then path B is not needed, in fact, it can create a cycle, produces unnecessary weight.
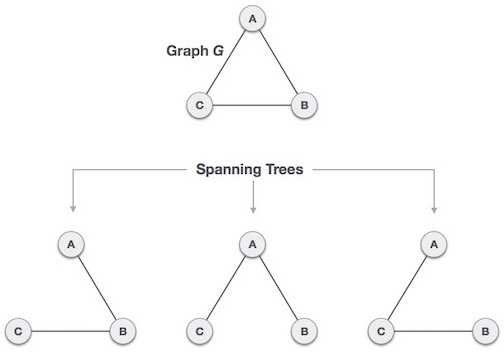
Image Source: https://www.tutorialspoint.com/data_structures_algorithms/images/spanning_trees.jpg
What is Minimum Spanning Tree?
Minimum Spanning Tree is a subset of a Graph, without any cycle. But it will be the best possible minimum cost spanning tree. What it means is, if you have to choose between two paths, minimum spanning tree always chooses the most efficient path.
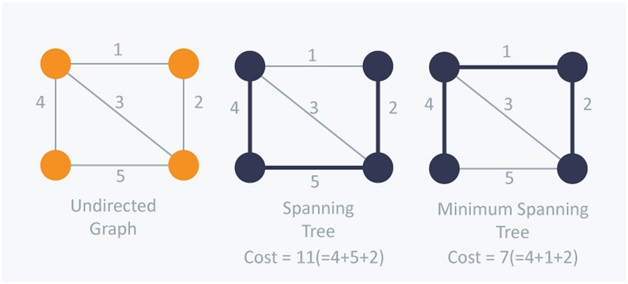
Image source: https://he-s3.s3.amazonaws.com/media/uploads/146b47a.jpg
What is Prim's Algorithm?
Prim's algorithm is a greedy algorithm that finds a minimum spanning tree for a weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. The algorithm operates by building this tree one vertex at a time, from an arbitrary starting vertex, at each step adding the cheapest possible connection from the tree to another vertex.
Reference: https://en.wikipedia.org/wiki/Prim%27s_algorithm.
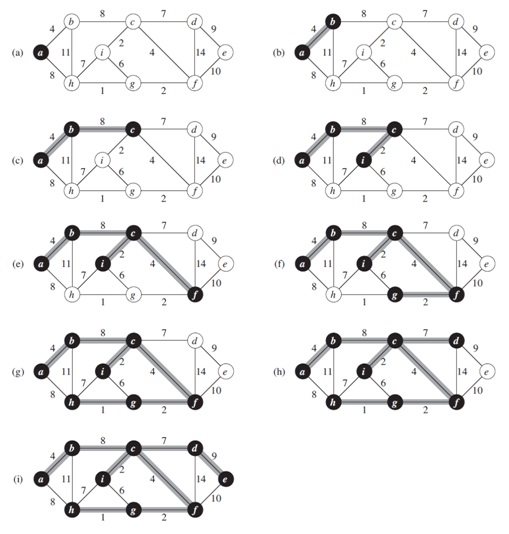
Image source: https://i.stack.imgur.com/TTwpR.png
C program for creating minimum spanning tree from Prim's algorithm
#include <stdio.h>
#define MAX 10
#define TEMP 0
#define PERM 1
#define FALSE 0
#define TRUE 1
#define infinity 9999
struct node {
int predecessor;
int dist; /*Distance from predecessor */
int status;
};
struct edge {
int u;
int v;
};
int adj[MAX][MAX];
int n;
/*This function returns TRUE if all nodes are permanent*/
int all_perm(struct node state[MAX]) {
int i;
for (i = 1; i <= n; i++)
if (state[i].status == TEMP) return FALSE;
return TRUE;
} /*End of all_perm()*/
int create_graph() {
int i, max_edges, origin, destin, wt;
printf("Enter number of vertices : ");
scanf("%d", &n);
max_edges = n * (n - 1) / 2;
for (i = 1; i <= max_edges; i++) {
printf("Enter edge %d(0 0 to quit) : ", i);
scanf("%d %d", &origin, &destin);
if ((origin == 0) && (destin == 0)) break;
printf("Enter weight for this edge : ");
scanf("%d", &wt);
if (origin > n || destin > n || origin <= 0 || destin <= 0) {
printf("Invalid edge!\n");
i--;
} else {
adj[origin][destin] = wt;
adj[destin][origin] = wt;
}
} /*End of for*/
if (i < n - 1) {
printf("Spanning tree is not possible\n");
return 1;
}
} /*End of create_graph()*/
void display() {
int i, j;
for (i = 1; i <= n; i++) {
for (j = 1; j <= n; j++) printf("%3d", adj[i][j]);
printf("\n");
}
} /*End of display()*/
int maketree(struct edge tree[MAX], int *weight) {
struct node state[MAX];
int i, k, min, count, current, newdist;
int m;
int u1, v1;
*weight = 0;
/*Make all nodes temporary*/
for (i = 1; i <= n; i++) {
state[i].predecessor = 0;
state[i].dist = infinity;
state[i].status = TEMP;
}
/*Make first node permanent*/
state[1].predecessor = 0;
state[1].dist = 0;
state[1].status = PERM;
/*Start from first node*/
current = 1;
count = 0; /*count represents number of nodes in tree */
while (all_perm(state) != TRUE) /*Loop till all the nodes become PERM*/
{
for (i = 1; i <= n; i++) {
if (adj[current][i] > 0 && state[i].status == TEMP) {
if (adj[current][i] < state[i].dist) {
state[i].predecessor = current;
state[i].dist = adj[current][i];
}
}
} /*End of for*/
/*Search for temporary node with minimum distance
and make it current node*/
min = infinity;
for (i = 1; i <= n; i++) {
if (state[i].status == TEMP && state[i].dist < min) {
min = state[i].dist;
current = i;
}
} /*End of for*/
state[current].status = PERM;
/*Insert this edge(u1,v1) into the tree */
u1 = state[current].predecessor;
v1 = current;
count++;
tree[count].u = u1;
tree[count].v = v1;
/*Add wt on this edge to weight of tree */
*weight = *weight + adj[u1][v1];
} /*End of while*/
return (count);
} /*End of maketree()*/
int main() {
int i, j;
int path[MAX];
int wt_tree, count;
struct edge tree[MAX];
create_graph();
printf("Adjacency matrix is :\n");
display();
count = maketree(tree, &wt_tree);
printf("Weight of spanning tree is : %d\n", wt_tree);
printf("Edges to be included in spanning tree are : \n");
for (i = 1; i <= count; i++) {
printf("%d->", tree[i].u);
printf("%d\n", tree[i].v);
}
return 0;
} /*End of main()*/
Output
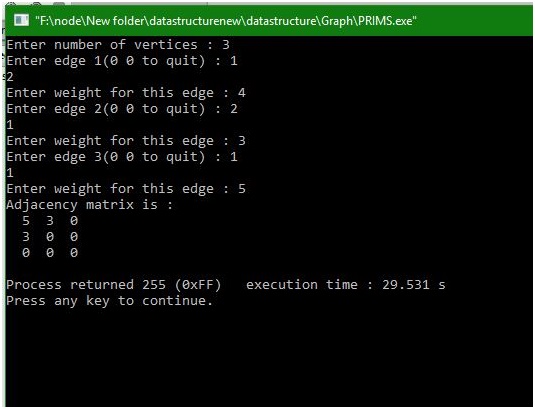
Advertisement
Advertisement