Home »
Data Mining
Association Analysis in Data Mining
Data Mining | Association Analysis: In this tutorial, we will learn about the association rule mining or association analysis in data mining.
By Palkesh Jain Last updated : April 17, 2023
What is Association Analysis?
Association analysis is most widely used to discover hidden patterns in large data sets. These hidden and uncovered relationships can be represented in the form of association rules or sets of frequent items. The role of identifying interesting associations in large databases is correlation analysis. There can be two types of these enthralling relationships: frequent itemsets or rules of the association. Frequent object sets are a collection of objects that mostly take place together. Association rules are the method of viewing fascinating relationships. The rules of association show that a close bond occurs between two or more objects.
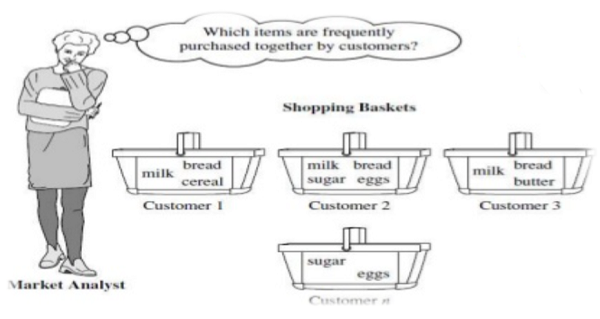
Fig: Market Basket Analysis
Market Basket Analysis
In transactional data, each case is connected with a set of objects. In principle, the list may contain all possible data items in the collection. For example - in a single market-basket analysis, goods with related items may be bought. However, only a small subset of all potential goods are present in a given set; only a small fraction of the items available for sale in the shop reflect the items in the market basket.
A common example of a regular pattern (item set) mining for association rules is market basket analysis. Business basket, the research analyzes the purchasing patterns of consumers by identifying correlations with the multiple items carried in their shopping baskets by customers.
An example of association rule - milk, bread
In a shop, if a shopkeeper sales milk then it is a probability to sell bread because a customer who is buying milk may also purchase bread. So it is showing that milk and bread are correlated with one another.
Association Rule
An associative rule is an example of the implication of the form X→YX→Y, where XX and YY are disjoint item sets (X∩Y=∅X∩Y=∅).
In terms of its support and trust, the strength of an alliance rule can be calculated. Legislation that has very low support will happen purely by chance. The reliability of the conclusion made by a rule is determined by trust.
Support of an association rule X→YX→Y
σ(X)σ(X) is the support count of XX
NN is the count of the transactions set TT.
s(X→Y)=σ(X∪Y)Ns(X→Y)=σ(X∪Y)N
Confidence of an association rule X→YX→Y
σ(X)σ(X) is the support count of XX
NN is the count of the transactions set TT.
conf(X→Y)=σ(X∪Y)σ(X)conf(X→Y)=σ(X∪Y)σ(X)
The interest of an association rule X→YX→Y
P(Y)=s(Y)P(Y)=s(Y) is the support of YY (fraction of baskets that contain YY)
If the interest of a rule is close to 1, then it is uninteresting.
I(X→Y)=1→XI(X→Y)=1→X and YY are independent
I(X→Y)>1→XI(X→Y)>1→X and YY are positively correlated
I(X→Y)<1→XI(X→Y)<1→X and YY are negative correlated
I(X→Y)=P(X,Y)P(X)×P(Y)I(X→Y)=P(X,Y)P(X)×P(Y)
For example, given a table of market basket transactions:
| TID |
Items |
| 1 |
{Bread, Milk} |
| 2 |
{Bread, Diaper, Beer, Eggs} |
| 3 |
{Milk, Diaper, Beer, Coke} |
| 4 |
{Bread, Milk, Diaper, Beer} |
| 5 |
{Bread, Milk, Diaper, Coke} |
We can conclude that,
s({Milk,Diaper}→{Beer})=2/5=0.4s({Milk,Diaper}→{Beer})=2/5=0.4
conf({Milk,Diaper}→{Beer})=2/3=0.67conf({Milk,Diaper}→{Beer})=2/3=0.67
I({Milk,Diaper}→{Beer})=2/53/5×3/5=10/9=1.11
Reference: Market Basket Analysis
Advertisement
Advertisement