Home » Data Structure

Find Height (Maximum Depth) of a Binary Search Tree (C++ program)

Learn: How to find the height or maximum depth of a binary search tree? This article includes definition, algorithm and implementation in C++ program.
Submitted by Abhishek Jain, on July 30, 2017

The Height (or depth) of a tree is defined to be the maximum level of any node in the tree. Some authors define depth of a node to be the length of the longest path from the root node to that node, which yields the relation:

Depth of the tree = Height of the tree - 1

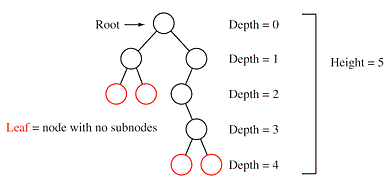
Reference: http://codersmaze.com/data-structure-explanations/trees-in-data-structure/

Algorithm:

FindHeight( Node root)
	If root=NULL 
		return 0
	Else
	int l=FindHeight (root->left)
	int r=FindHeight(root->right) 
	Return max(l,r)+1
	[End If]
[End]

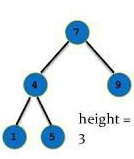
Consider the program:

#include<iostream>
using namespace std;

struct node
{
	int data;
	node* left;
	node* right;
};

struct node* getNode(int data)
{
	node* newNode=new node();
	newNode->data=data;
	newNode->left=NULL;
	newNode->right=NULL;
	return newNode;
}

void inorder(struct node* root)
{
	if (root != NULL)
	{
		inorder(root->left);
		cout<<root->data<<" ";
		inorder(root->right);
	}
}

struct node* Insert(struct node* root, int data)
{
	if (root == NULL)
		return getNode(data);

	if (data < root->data)
		root->left  = Insert(root->left, data);
	else if (data > root->data)
		root->right = Insert(root->right, data);

	return root;
}

int FindHeight(node* root)
{
	if(root==NULL)
		return 0;

	else
	{
		int lb=FindHeight(root->left);
		int rb=FindHeight(root->right);
		return max(lb,rb)+1;
	}
}
int main()
{
	node* root=NULL;
	root=Insert(root,7);
	Insert(root,9);
	Insert(root,4);
	Insert(root,1);
	Insert(root,5);

	cout<<"Inorder: ";
	inorder(root);
	cout<<endl;

	cout<<"Height of the tree is "<<FindHeight(root)<<endl;
	cout<<"Max. Depth of the tree is "<<FindHeight(root)-1;
	
	return 0;
}

Output

Inorder: 14579
Height of the tree is 3
Max. Depth of the tree is 2