Home » Python » Linear Algebra using Python

Binomial Process | Linear Algebra using Python

Linear Algebra using Python | Binomial Process: Here, we are going to learn about the binomial process and its implementation in Python.
Submitted by Anuj Singh, on June 13, 2020

When we flip a coin, there are two possible outcomes as head or tail. Each outcome has a fixed probability of occurrence. In the case of fair coins, heads and tails each have the same probability of 1/2. In addition, there are cases in which the coin is biased, so that heads and tails have different probabilities of occurrence. Coin toss experiment for number of n trails can be called as a binomial distribution.

As per Wikipedia Definition: In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent experiments, each asking a yes–no question, and each with its own boolean-valued outcome: success/yes/true/one (with probability p) or failure/no/false/zero (with probability q = 1 − p). A single success/failure experiment is also called a Bernoulli trial or Bernoulli experiment and a sequence of outcomes is called a Bernoulli process; for a single trial, i.e., n = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the popular binomial test of statistical significance.

Here, we will learn to create a binomial distribution using python with Probability parameter p = 0.1.

Python code for Binomial Process

# Linear Algebra Learning Sequence
# Binomial Process

import pylab as pl

# defining factorial function
k = 0
def fact(num):
    facto = 1
    while num>0:
        facto = facto*num
        num = num - 1
    return facto    
# print(fact(5)) #// for checking


# Defining power function
def exp(num,po):
    ex = 1
    while po>0:
        ex = ex*num
        po = po - 1
    return ex    
# print(exp(2,8)) #// for checking


# Implementation of Binomial Process 
# Probability of K arrivals with 
# probability of arrival as pr
# not arrival probability is 1-pr
# P = n!/(n-r)!*r! * p^r * (1-p)^n-r
# r = k

def Binomial(N,k,pr):
    BinCoef = (fact(N)/(fact(N-k)*fact(k)))
    ProRatio = (exp(pr,k)*exp(1-pr,N-k))
    Probability = BinCoef*ProRatio
    
    return Probability

N = 1
n = 1
k = 1
pr = 0.1
prn = 0.9

# Use of Vector to save data and 
# further algebric manipulation
x = []  
y = []

while n<40:
    x.append(n)
    y.append(Binomial(n,k,pr))
    n = n + 1

pl.plot(x,y)

print('Binomial Process Vector : ', y)

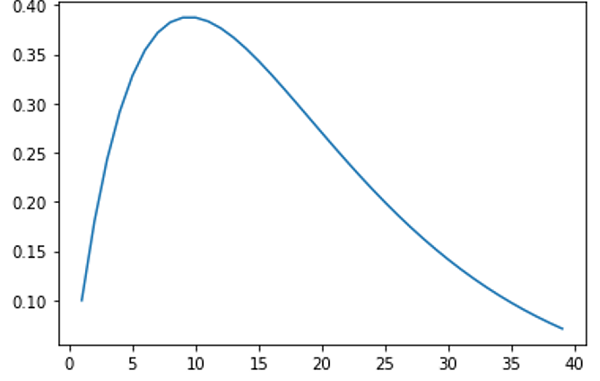
Output:

Binomial Process Vector :  [0.1, 0.18000000000000002, 0.24300000000000005, 
0.2916, 0.32805000000000006, 0.3542940000000001, 0.37200870000000014, 
0.3826375200000001, 0.38742048900000015, 0.3874204890000002, 
0.3835462841100002, 0.37657271530800024, 0.36715839742530026, 
0.3558612159660602, 0.3431518868244152, 0.32942581135143856, 
0.3150134321048131, 0.3001892705939984, 0.2851798070642985, 
0.27017034353459857, 0.25531097464019564, 0.24072177608932738, 
0.22649730750223074, 0.2127105148716602, 0.19941610769218143, 
0.18665347679988184, 0.17444921100912034, 0.16281926360851232, 
0.1517708135779347, 0.14130386091738747, 0.13141259065317037, 
0.1220865358326228, 0.11331156606965304, 0.10507072490095098, 
0.09734493630529284, 0.09011359817975681, 0.08335507831627505, 
0.07704712644369205, 0.07116721416246292]