Home » Python » Python Programs

Breadth First Search for a Graph in Python

Python | Breadth First Search: In this tutorial, we will learn about the breadth first search algorithm and its implement for a graph in Python. By Soumya Sinha Last updated : April 21, 2023

A Breadth-first search algorithm is often used for traversing/searching a tree/graph data structure.

Here, we will learn to implement BFS Algorithm for a graph.

BFS Algorithm for a Graph

BFS for a graph is almost similar to BFS of a tree. There is only one difference here, unlike trees graphs may contain cycles, so it may happen that we come across the same vertex again and again. A vertex needs to be processed only once, so to avoid this situation we will use an array to keep track of the state of the vertex.

For example, in the following graph, suppose we start traversing from vertex A. When we come to vertex B, we look for all adjacent vertices of it. A is also an adjacent vertex of B. If we don't keep track of the visited vertices, then A will be processed again and again, hence this will become a non-terminating process.

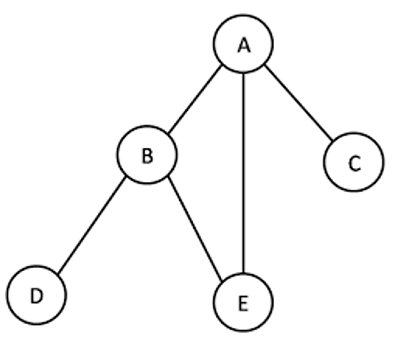
Description

In this algorithm we need to discover vertices in order of distance from the source vertex. This breadth first search algorithm works for both directed and undirected graphs.

Data Structures Used

• state[u]: Provides the colour status of a node during the BFS operation.
  • If state[u] = 1, then the node has not been discovered yet.
  • If state[u] = 0, then the node has been discovered but not processed yet.
  • If state[u] = 0, then the node has been processed.
• distance[u]: Stores the distance of a vertex from the source vertex S
• parent[u]: Stores the parent information

Procedure for BFS Algorithm for a Graph

The procedure of BFS algorithm for a graph is as follow,

BFS(G, s)
    #Initialize all the vertex except the source vertex
    #V[graph] – list of nodes in the graph
    for each vertex u ε V [Graph] - {s}
        do state[u] = 1
        distance[u] = 'inf' 
        parent[u] = nil
    #Initialize the source vertex
    state[s] = 0
    distance[s] = 0
    parent[s] = nil
    #Create an empty Queue and an array arr to store the result 
    queue = []
    arr = []
    #Insert the source vertex in the queue
    Enqueue(queue, s) 
    #loop until queue is empty
    while queue  
        do u 🡨  Dequeue(queue) 
        for each v ε Adjacent[u] 
            do if state[v] = 1 
                then state[v] =  0 
                distance[v] = distance[u]+1 
                parent[v] =  u 
                Enqueue(queue, v) 
        state[u] = -1

Time Complexity

Time Complexity of BFS = O(V+E) where V is number of vertices and E is number of edges.

Python program to implement breadth first search for a graph

import sys
import math

def bfs(n, edges, s):
    #initialize state, distance and parent for all the vertices
    state = [0 for i in range(n)]
    distance = [float('inf') for i in range(n)]
    parent = [-1 for i in range(n)]
    #initialize state, distance and parent for the source vertex
    state[s] = 1 
    distance[s] = 0 
    parent[s] = 'NIL'
    queue = []
    arr = []
    queue.append(s)
    #Start discovering the vertices starting from the source vertex
    while queue:
        x = queue.pop(0)
        arr.append(x)
        #Start discovering the vertices adjacent to x and store
        #information about their parent, distance and state
        for i in range(len(edges[x])):
            if state[edges[x][i]] == 0:
                state[edges[x][i]] = 1 
                distance[edges[x][i]] = distance[x] + 1
                parent[edges[x][i]] = x 
                queue.append(edges[x][i])
        state[x] = -1
 
    return arr 
 
def main():
   #input format is described below
    n, m, s = map(int, input().split())
    edges = {}
    for i in range(n):
        edges[i] = []
    for i in range(m):
        a, b = map(int, input().split())
        edges[a] += [b]
        edges[b] += [a]
    for i in range(n):
        edges[i].sort()
    arr = bfs(n, edges, s)
    print(*arr)
 
if __name__ == '__main__':
    main()

Input

Input format:

• First line of input contains the integers n, m s where
  • n = number of nodes
  • m = number of edges
  • s = source node
• Next m lines contain two integers which specifies that the vertices are connected by an edge

9 13 0
0 1
0 7
1 7
1 2
2 3
2 5
2 8
3 4
3 5
4 5
5 6
6 7
7 8

Output

Output Format: Breadth first traversal starting from source node

0 1 7 2 6 8 3 5 4

Python Data Structure Programs »