Home » Python » Linear Algebra using Python

Python | One Hidden Layer Simplest Neural Network

In this article, we are going to learn about the one hidden layer simplest neural network and its Python implementation?
Submitted by Anuj Singh, on July 11, 2020

A neural network is a powerful tool often utilized in Machine Learning because neural networks are fundamentally very mathematical. We will use our basics of Linear Algebra and NumPy to understand the foundation of Machine Learning using Neural Networks. Our article is a showcase of the application of Linear Algebra and Python provides a wide set of libraries that help to build our motivation of using Python for machine learning.

The figure is showing a neural network with two input nodes, one hidden layer, and one output node.

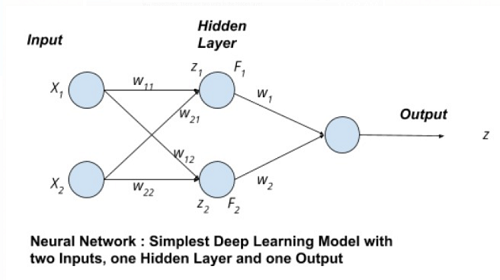
Input to the neural network is X1, X2, and their corresponding weights are w11, w12, w21, and w21 respectively. There are two units in the hidden layer.

1. For unit z1 in hidden layer:

   F1 = tanh(z1) 
   F1 = tanh(X1.w11 + X2.w21)
   

2. For unit z2 in hidden layer:

   F1 = tanh(z2)
   F2 = tanh(X2.w12 + X2.w22)                                         
   

The output z is a tangent hyperbolic function for decision making which has input as the sum of products of Input and Weight. Mathematically, z = tanh(∑F_iw_i)

Where tanh() is an tangent hyperbolic function because it is one of the most used decision-making functions. So for drawing this mathematical network in a python code by defining a function neural_network(X, W).

Note: The tangent hyperbolic function takes input within a range of 0 to 1.

Input Parameter: Vector X, W and w

Return: A value ranging between 0 and 1, as a prediction of the neural network based on the inputs.

Application:

1. Machine Learning
2. Computer Vision
3. Data Analysis
4. Fintech

Python code for one hidden layer simplest neural network

# Linear Algebra and Neural Network
# Linear Algebra Learning Sequence

import numpy as np

# Use of np.array() to define an Input Vector
V = np.array([.323,.432])
print("The Vector A as Inputs : ",V)

# defining Weight Vector
VV = np.array([[.3,.66,],[.27,.32]])
W = np.array([.7,.3,])

print("\nThe Vector B as Weights: ",VV)

# defining a neural network for predicting an 
# output value
def neural_network(inputs, weights):
    wT = np.transpose(weights)
    elpro = wT.dot(inputs)
    
    # Tangent Hyperbolic Function for Decision Making
    out = np.tanh(elpro)
    return out

outputi = neural_network(V,VV)

# printing the expected output
print("Expected Value of Hidden Layer Units: ", outputi)

outputj = neural_network(outputi,W)

# printing the expected output
print("Expected Output of the with one hidden layer : ", outputj)

Output:

The Vector A as Inputs :  [0.323 0.432]

The Vector B as Weights:  [[0.3  0.66]
 [0.27 0.32]]
Expected Value of Hidden Layer Units:  [0.21035237 0.33763427]
Expected Output of the with one hidden layer :  0.24354287168861996