Home » Python » Linear Algebra using Python

Python | Vandermonde Matrix

Vandermonde Matrix in Python: Here, we are going to learn about the vandermonde matrix and its implementation in Python.
Submitted by Anuj Singh, on July 17, 2020

A Vandermonde Matrix is a square matrix (having size nxn), if and only if there are scalars, x₁, x₂ , x₃,…, x_n  such that,

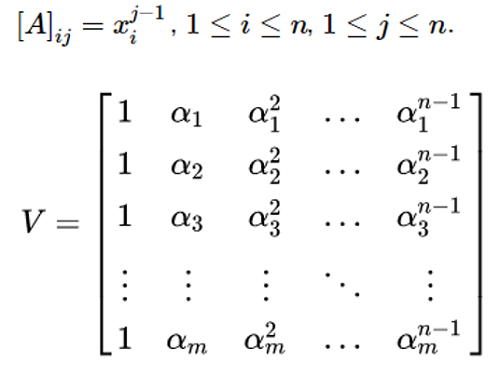
Source: https://en.wikipedia.org/wiki/Vandermonde_matrix

Python numpy package allows us to create a Vandermonde Matrix by providing an inbuilt function numpy.vander().

Python code for vandermonde matrix

# Linear Algebra Learning Sequence
# Vandermonde Matrix

import numpy as np

x = np.array([1, 2, 3, 5])
N = 3
v1 = np.vander(x)

print('Vector x :\n', x)
print('Vandermonde Matrix of vector x', v1)

y = np.array([4,5,6,7,8,9])
N = 4
v2 = np.vander(y, N)
v3 = np.vander(y)

print('\n\nVector y :\n', y)
print('Vandermonde Matrix of vector y (N = 4): ', v2)
print('\n\n Vandermonde Matrix (Square) of vector y : ', v3)

Output:

Vector x :
 [1 2 3 5]
Vandermonde Matrix of vector x [[  1   1   1   1]
 [  8   4   2   1]
 [ 27   9   3   1]
 [125  25   5   1]]


Vector y :
 [4 5 6 7 8 9]
Vandermonde Matrix of vector y (N = 4):  [[ 64  16   4   1]
 [125  25   5   1]
 [216  36   6   1]
 [343  49   7   1]
 [512  64   8   1]
 [729  81   9   1]]


 Vandermonde Matrix (Square) of vector y :  [[ 1024   256    64    16     4     1]
 [ 3125   625   125    25     5     1]
 [ 7776  1296   216    36     6     1]
 [16807  2401   343    49     7     1]
 [32768  4096   512    64     8     1]
 [59049  6561   729    81     9     1]]