C++ program to check whether a given Binary Search Tree is balanced or not?

In this tutorial, we will learn how to implement a C++ program that will check whether a given binary search tree is a balanced tree or not? By Bhanu Pratap Raghav Last updated : August 10, 2023

Problem description

Solution to check the given Binary Search tree is balanced or not.

Problem statement

Write a C++ program that accepts input from user to form a binary search tree and check whether the formed tree is balanced or not.

Example 1

Input: 2 1 3 4 5 -1

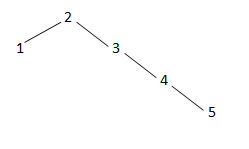
Output: Given BST is Balanced : False

Example 2

Input: 2 1 3 4 -1

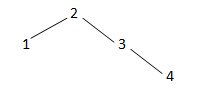
Output: Given BST is Balanced : True

What do you mean by height of a tree?

A height of a tree is the largest number of edges in a path from node to a leaf node. If a tree has only one node: i.e. root node itself then the height of tree is 0.

Example:

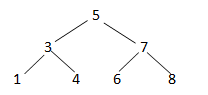
Height of tree: 2 ( maximum 2 edges from root to leaf)

Check when tree is balanced

A non-empty binary search tree is said to be balanced if:

Its left subtree is balanced.
Its Right subtree is balanced.
The difference between heights of left and right subtree is less than or equal to 1.

Example:

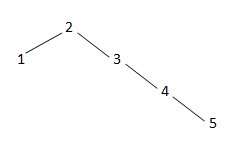
At root height of left subtree is 1 , whereas height of right subtree is 3

Difference = 3-1=2 (which is greater than 1) i.e. Tree is not balanced.

Algorithm

Set root=root of given binary search tree.
Set leftHt= height of left subtree.
Set rightHt= height of right subtree.
if abs(leftHt – rightHt ) > 1
return false;
else isHeightBalanced(root->left) &&isHeightBalanced(root->right)

C++ program to check whether a given Binary Search Tree is balanced or not?

#include <iostream>
#include <cmath>

using namespace std;

class TreeNode {
public:
    int data;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int d)
    {
        data = d;
        left = NULL;
        right = NULL;
    }
};

TreeNode* insertInBST(TreeNode* root, int x)
{
    if (root == NULL) {
        TreeNode* tmp = new TreeNode(x);
        return tmp;
    }

    if (x < root->data) {
        root->left = insertInBST(root->left, x);
        return root;
    }
    else {
        root->right = insertInBST(root->right, x);
        return root;
    }
}

TreeNode* createBST()
{
    TreeNode* root = NULL;
    int x;
    cin >> x;

    //Take input until user inputs -1
    while (true) {
        if (x == -1)
            break;
        root = insertInBST(root, x);
        cin >> x;
    }
    return root;
}

//Calculate height of tree with given root
int height(TreeNode* root)
{
    if (root == NULL)
        return 0;

    int leftHt = height(root->left);
    int rightHt = height(root->right);
    int curHt = max(leftHt, rightHt) + 1;
    return curHt;
}

//Check whether tree is balanced or not
bool isHeightBalanced(TreeNode* root)
{
    if (!root) {
        return true;
    }

    int leftHt = height(root->left);
    int rightHt = height(root->right);

    if (abs(leftHt - rightHt) > 1)
        return false;
    return isHeightBalanced(root->left) && isHeightBalanced(root->right);
}

int main()
{
    //Input BST
    cout << "Input Tree elements : ";
    TreeNode* root = createBST();

    cout << "Given BST is Balanced : ";
    if (isHeightBalanced(root)) {
        cout << "True";
    }
    else {
        cout << "False";
    }

    return 0;
}

Output

First run:
Input Tree elements(stop taking input when  -1 encountered) : 2 1 3 4 5 -1
Given BST is Balanced : False

Second run:
Input Tree elements(stop taking input when  -1 encountered) : 2 1 3 4  -1
Given BST is Balanced : True