Topological sort implementation using C++ program

Topological sort implementation: In this tutorial, we will learn about the Topological sort, its example, its algorithm, and the implementation of Topological sort using the C ++ program. By Souvik Saha Last updated : August 09, 2023

Problem statement

Given a graph of n vertices, you have to topologically sort that graph.

Example

Input:

If there is graph be like the below:

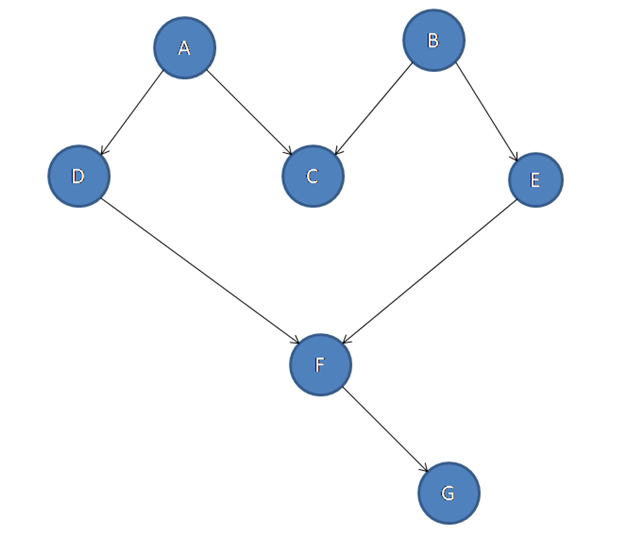
Output: A → B → C → D → E → F → G

Topological sort

It is a technique where each node comes after it's parent node.

Here, node A and node B are two nodes which have no parents. So A comes first then D node comes but to print F we need D and E both the nodes so it is not possible. Then comes node B and node C also available and then E, F and G come.

Topological sort algorithm

The steps to implement topological sort algorithm are:

We take two stacks and a set. We use the set to mark the nodes.
We start with any of the vertexes and push it into the stack and mark it (insert into the set).
We take the top element and check for its unvisited adjacent vertices if it exists then push it into the stack and if not then all the nodes are visited therefore we pop that node from the stack and place it into the other stack.
We repeat step 3 until we visited all the nodes.

C++ program to implement topological sort

#include <bits/stdc++.h>
using namespace std;

void addedge(list<int>* ls, int x, int y)
{
    ls[x].push_back(y);
}

string topological_sort(list<int>* ls, int k)
{
    char arr[k];
    stack<int> s;
    set<int> st;
    int ind = k - 1;
    
    for (int i = k - 1; i >= 0; i--) {
        if (st.find(i) == st.end()) {
            s.push(i);
            st.insert(i);
            
            //check all the non visited nodes
            while (!s.empty()) {
                int p = s.top();
                list<int>::iterator it;
                int temp = 0;
                
                //check its adjacent non visited nodes
                for (it = ls[p].begin(); it != ls[p].end(); it++) {
                    if (st.find(*it) == st.end()) {
                        st.insert(*it);
                        s.push(*it);
                        temp = 1;
                    }
                }
                
                //if all adjaceny nodes are visited then pop that element from stack
                if (temp == 0) {
                    char ch = (char)(p + 'A');
                    arr[ind] = ch;
                    ind--;
                    s.pop();
                }
            }
        }
    }
    return arr;
}

int main()
{
    int k = 7;
    list<int> ls[k];
    
    addedge(ls, 0, 2);
    addedge(ls, 0, 3);
    addedge(ls, 1, 2);
    addedge(ls, 1, 4);
    addedge(ls, 4, 5);
    addedge(ls, 3, 5);
    addedge(ls, 5, 6);
    
    cout << topological_sort(ls, 7) << endl;
    
    return 0;
}

Output

ABCDEFG