C++ program to find number of BSTs with N nodes (Catalan numbers)

Catalan numbers using C++: In this tutorial, we will learn how to implement a C++ program to find the number of BSTs with N Nodes (Catalan numbers). By Saksham Bhayana Last updated : August 10, 2023

Problem statement

Write a C++ program to find the number of BSTs with N Nodes (Catalan numbers).

Consider the below-given example with sample input and output -

Input format: single integer n
Constraints: 0=<n<=15
Sample input: 4
Sample output: 14 binary search tree/trees are there for 4 nodes

Example with explanation

The number of BSTs with n vertices is given by Catalan numbers. For n=0,1,2,3,4... Catalan numbers are 1,1,2,5,14... and so on.

Catalan numbers are given by Cn = (2n)!/(n+1)!*n! = count of BSTs with nodes n.

Catalan numbers are used here to find the count of BSTs because both satisfy same recurrence relation that is:

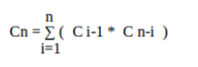
For n=0 number of trees is 1 i.e. empty tree. For subsequent values:

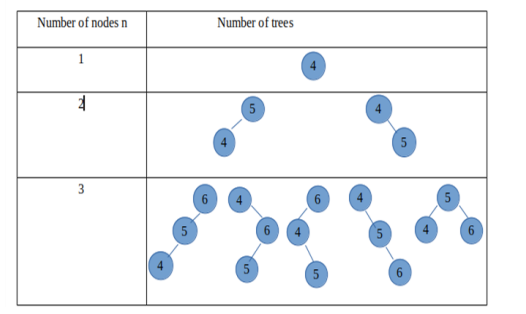
And, so on...

Finding number of BSTs with N nodes (Catalan numbers)

If we consider root as the i^th node then:

i-1 nodes are there in left subtree.
n-i nodes are there in right subtree.

Let’s denote count of BST by Bn for n elements

The 2 subtrees here will be independent of each other. Therefore it will be ( B i-1 * B n-i ) for Bi . For n nodes (as i has n choices) it will be :

Since the recurrence relation is same as of catalan numbers , so count of BST is given by Cn.

Recurrence relation:

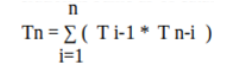
This gives complexity O(4^n). Complexity can be reduced to O(n^2) by using DP.

C++ program to find the number of BSTs with N Nodes (Catalan numbers)

#include <iostream>
using namespace std;

// Function to find number of BSTs with N nodes
// (Catalan numbers)
int CN(int n)
{
    int Cn = 0;
    // base case
    if (n == 0) // empty tree
    {
        return 1;
    }
    for (int i = 1; i < n + 1; i++) {
        Cn += CN(i - 1) * CN(n - i);
    }
    return Cn;
}

// main function starts
int main()
{
    int n;

    // Input
    cout << "Enter number of nodes: ";
    cin >> n;

    // Printing n
    cout << n << endl;

    // Finding the numbers
    int trees = CN(n);

    // Printing
    cout << trees << " binary search trees are there for " << n << " nodes" << endl;

    return 0;
}

Output

RUN 1:
Enter number of nodes: 4
4
14 binary search trees are there for 4 nodes

RUN 2:
Enter number of nodes: 6
6
132 binary search trees are there for 6 nodes

RUN 3:
Enter number of nodes: 2
2
2 binary search trees are there for 2 nodes