Home » Python » Python programs

Python program for double dice (one biased one normal) simulation

Double dice (one biased one normal) simulation in Python: Here, we are going to learn how to simulate the occurrence of the sum of the faces of two dice [i.e. dice(A) - 1, 2, 3, 4, 5 ,6 + dice(B) - 1, 2, 3, 4, 4, 4, 5, 6, 6 ,6]?
Submitted by Anuj Singh, on August 01, 2019

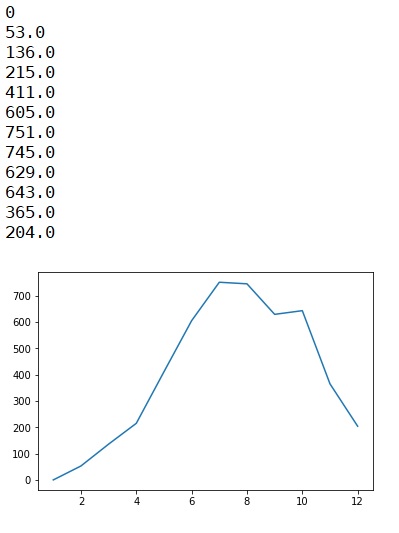
Here, we will be simulating the occurrence of the sum of the faces of two dice [i.e. dice(A) - 1, 2, 3, 4, 5 ,6 + dice(B) - 1, 2, 3, 4, 4, 4, 5, 6, 6 ,6]. A dice is normal(each has an equal probability of occurrence) and another B dice is biased one (each face has not an equal probability of outcome). So, in this case, we have to find out the maximum probable sum if the dice. So we simply take the help of stimulation to do so. Simply we are going to use an inbuilt library called as random to call a random value from given set and thereby we can stimulate the occurrence value by storing the occurrence in the list ls of length 12 representing each face of the dice as ls[4] represents the occurrence of face 5.

    ls[0]   - dice(1)
    ls[1]   - dice(2)
    ls[2]   - dice(3)
    ls[3]   - dice(4)
    ls[3]   - dice(5)
    ls[5]   - dice(6) 
    ls[6]   - dice(7)
    ls[7]   - dice(8)
    ls[8]   - dice(9)
    ls[9]   - dice(10)
    ls[10]  - dice(11)
    ls[11]  - dice(12) 

Then using the library pylab, we can plot the value of each occurrence and can stimulate it.

The deviation is clear that each of the faces has an equal almost equal probability of occurrence.

Program:

import random
import pylab as py

def roll():
    return random.choice([1,2,3,4,5,6])

def biased():
    return random.choice([1,2,3,4,4,4,5,5,5,6,6,6])

ls = [0,0,0,0,0,0,0,0,0,0,0,0]
chance = [104, 203, 302, 401, 505, 646, 756, 855, 985]
for n in chance:
    for k in range(n):
        scr = roll() + biased() 
        ls[scr-1] = ls[scr-1] + 4/4


py.figure()
py.plot([1,2,3,4,5,6,7,8,9,10,11,12], ls)

for el in ls:
    print(el)

Output