C program to implement heap sort algorithm

Heap Sort Algorithm Implementation: In this tutorial, we will learn about the heap sort algorithm, how it works, and the implementation of the heap sort algorithm using the C program. By Sneha Dujaniya Last updated : August 03, 2023

Heap Sort

Heap Sort is a comparison-based sorting algorithm that makes use of a different data structure called Binary Heaps. Let us understand some important terms,

Complete Binary Tree: A tree is complete when all the levels (except of course the last level) are completely filled, i.e. all the parent nodes have two children nodes each and all the nodes are as far left as possible which means first we fill the left node and then the right.
Binary Heap: It is a complete binary tree but there is an order of elements from parent to children in Binary Heap. They can be of two types,
1. Max Binary Heap or Max Heap where the parent node is greater than its two children nodes.
2. Min Binary Heap or Min Heap where the parent node is smaller than its children nodes.

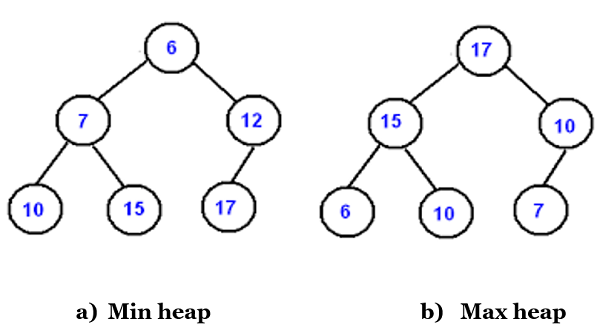
The main() function of Heap Sort is to call the heapify() function which leads to the building of a max heap and then the largest element is stored in the last position of the array as so on till only one element is left in the heap. Array representation of heap is preferred because it occupies less space and also it is easy to reference the root and children nodes.

Algorithm (Considering Max Heap)

First, we form a Max Heap such that the first node or the root node is the largest element. This step takes O(N) time complexity.
Next, we swap the root element with the last element of the heap and reduce the size of heap by 1.
Repeat steps 1 and 2 are till only 1 element is left.

How to build the Heap?

The heapify procedure can be applied to a node only when its children nodes are heapified. Therefore, we start the heapification with the last non-leaf node. To find the first non-leaf node, the following formula is used: First non-leafy node = lower bound (n/2)

Hence, if there are 5 elements in the heap, the first non-leafy node would be the second node or the node at index 1.

Pseudo Code

Heap_Sort (arr[], n)
{
     // Creating the initial Max heap
     for i = n/2 – 1 to 0:
        heapify(arr, n, i)

     // Swapping largest element and repeating the steps further
     for i = n-1 to 0:
        swap(arr[0], arr[i]
        heapify(arr, n, i)
}

Heapify (arr[], n, i)
{
     int largest = i;
     int left = 2*i + 1; // Left child
     int right = 2*i + 2; // Right child

     // Check if left child exists and is larger than root
     If (left < n && arr[left] > arr[largest]):
        Largest = left;
     
     // Check if right child exists and is larger than largest
     If (right < n && arr[right] > arr[largest]):
        largest = right;
     
     // Change root, if root is not the largest
     If(largest != i)
        Swap(arr[i], arr[largest])
        Heapify(arr, n, largest); //Repeat till max heap is obtained
}

Time Complexity

The time complexity of Heap sort is:

Worst Case = O(N log N)
Average Case = Ɵ(N log N)
Best Case = Ω(N log N)
Space Complexity: Ɵ(1)

The time complexity of Heapify is O(log N) and that of Build_heap / Heap_Sort is O(N). The overall complexity of Heap_Sort is therefor, O(N log N).

C program to implement heap sort algorithm

#include <stdio.h>

void swap(int* a, int* b)
{
    int temp = *a;
    *a = *b;
    *b = temp;
}

void heapify(int arr[], int n, int i)
{
    int left, right, largest;
    largest = i;
    left = 2 * i + 1;
    right = 2 * i + 2;

    // Check if left child exists and is larger than its parent
    if (left < n && arr[left] > arr[largest])
        largest = left;
    // Check if right child exists and larger than its parent
    if (right < n && arr[right] > arr[largest])
        largest = right;

    // if root is not the largest
    if (largest != i) {
        swap(&arr[i], &arr[largest]); //make root the largest
        heapify(arr, n, largest); // Apply heapify to the largest node
    }
}

void heap_sort(int arr[], int n)
{
    int i;
    for (i = (n / 2) - 1; i >= 0; i--)
        heapify(arr, n, i);

    for (i = n - 1; i >= 0; i--) {
        swap(&arr[0], &arr[i]); //Move the largest element at root to the end
        heapify(arr, i, 0); //Apply heapify to reduced heap
    }
}

int main()
{
    int arr[] = { 20, 13, 34, 56, 12, 10 };
    int n = sizeof(arr) / sizeof(arr[0]);

    printf("Array:\n");
    for (int i = 0; i < n; i++)
        printf("%d ", arr[i]);
        
    heap_sort(arr, n);

    printf("\nAfter performing Heap Sort:\n");
    for (int i = 0; i < n; i++)
        printf("%d ", arr[i]);

    return 0;
}

Output

Array:
20 13 34 56 12 10
After performing Heap Sort:
10 12 13 20 34 56

Applications

Job Scheduling: In Linux OS is used due to low space and time complexity
Graph Algorithms: Djikstar's Algorithm, Prim's Algorithm and Huffman Coding