C program to implement merge sort algorithm

Merge sort algorithm implementation: In this tutorial, we will learn about the merge sort algorithm, how it works, and implementation of merge sort algorithm using C program. By Sneha Dujaniya Last updated : August 03, 2023

Merge sort is an algorithm based on the divide and conquer paradigm which was invented by John von Neumann in the year 1945. It is a stable but not an in-place sorting algorithm.

A stable sorting algorithm is the one where two keys having equal values appear in the same order in the sorted output array as it is present in the input unsorted array.
An in-place sorting algorithm has various definitions but a more used one is – An in-place sorting algorithm does not need extra space and uses the constant memory for manipulation of the input in-place. Although, it may require some extra constant space allowed for variables.

Merge sort

Merge sort calls two functions. One is the MergeSort() wherein it recursively calls itself for dividing the array into two sub halves till each sub-array has only one element in it and hence, sorted. Then secondly, it calls the merge() function where it merges the two sorted sub halves or sub-arrays into one till only one entire list is obtained.

Pseudo code

Merge_Sort(arr[], l, r)
    If r > l:
    1.  Find the middle element in the list to divide it into two sub-arrays: 
        mid = (l + r)/2
    2.  Call Merge_Sort for first sub-array:
        Call Merge_Sort (arr, l, mid)
    3.  Call Merge_Sort for second sub_array:
        Call Merge_Sort(arr, mid+1, r)
    4.  Merge the two sub_arrays sorted in steps 2 and 3:
        Call Merge(arr, l, mid, r)

Example with explanation

Input array: 2 6 1 9
1.  Split the list into N sub lists: 
    (2) (6) (1) (9). 
    Hence, each list is sorted as there is only one element.
2.  Merge the list in pairs starting from index 0.
    Merge (2) (6): (2 6)
    Merge (1) (6): (1 6)
    Merge (2 4) (1 6)

3.	Merge two lists (2 4) (1 6): 
    Compare each element of 1st list with all the elements 
    of list 2 and insert the smaller one in a new list.

    Compare 2 and 1: 1 < 2, insert 1 in the new list first
    Compare 2 and 6: 2 < 6, insert 2 in the new list
    Compare 4 and 6: 4 < 6, insert 4 in the new list
    Insert 6 as it is the only element left
    List: (1 2 4 6) 

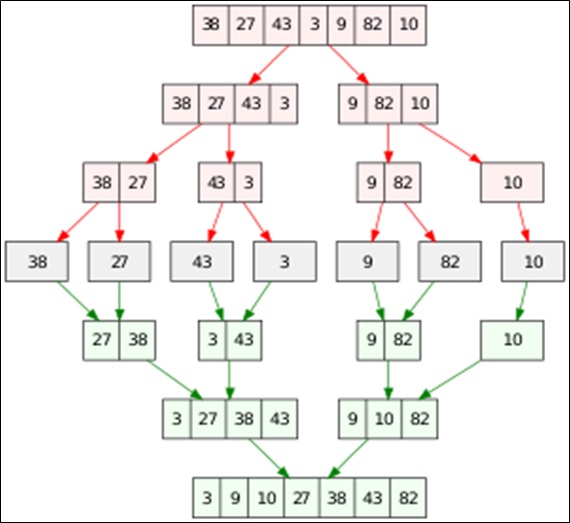
    See this image for better understanding of the concept. 
    The numbers represent the order in which the functions are called.
    (Source: Wikipedia)

Time complexity

The time complexity of the Merge Sort algorithm is defined by the following recurrence relation T(n) = 2T(n/2) + Ɵ(n) where Ɵ(n) is the time complexity of Merge function and is linear.

The above recurrence relation is solved using the Master's Theorem to obtain the time complexity. The complexity is the same in all the cases because unlike Quick Sort, Merge Sort always divides the array into two equal subparts.

Worst case: O(N log N)
Average Case: Ɵ(N log N)
Best case: Ω(N log N)
Space Complexity: Ɵ(N)

C program to implement merge sort algorithm

#include <stdio.h>

void merge(int arr[], int l, int mid, int r)
{
    int i, j, k;
    int m = mid - l + 1; // Number of elements in first sub array
    int n = r - mid; // Number of elements in second half

    // create temporary arrays and copy the actual data to these for comparison
    int A[20], B[20];
    for (i = 0; i < m; i++)
        A[i] = arr[l + i];
    for (j = 0; j < n; j++)
        B[j] = arr[mid + 1 + j];

    // Now, merge these temporary arrays after comparison
    i = 0;
    j = 0;
    k = l;
    while (i < m && j < n) {
        if (A[i] <= B[j]) {
            arr[k] = A[i];
            i++;
        }
        else {
            arr[k] = B[j];
            j++;
        }
        k++;
    }

    // This step is done if any of the list has left out elements
    while (i < m) {
        arr[k] = A[i];
        i++;
        k++;
    }
    while (j < m) {
        arr[k] = B[j];
        j++;
        k++;
    }
}

void merge_sort(int arr[], int l, int r)
{
    if (l < r) {
        // This method helps to avoid
        // overflow for large l and r
        int mid = l + (r - l) / 2;

        merge_sort(arr, l, mid); // Call for first half
        merge_sort(arr, mid + 1, r); // Call for second half
        merge(arr, l, mid, r); // Calling merge function
    }
}

int main()
{
    int arr[] = { 3, 8, 12, 9, 5, 26 };
    int n = sizeof(arr) / sizeof(arr[0]);

    printf("Array:\n");
    for (int i = 0; i < n; i++)
        printf("%d ", arr[i]);
        
    merge_sort(arr, 0, n - 1);

    printf("\nAfter performing the merge sort:\n");
    for (int i = 0; i < n; i++)
        printf("%d ", arr[i]);

    return 0;
}

Output

Array:
3 8 12 9 5 26
After performing the merge sort:
1 3 5 8 12 26