Home »
Digital Electronics
Computer Number Systems and Its Types
In this tutorial, we will learn about the computer number systems, its types, and number system conversions.
By IncludeHelp Last updated : May 10, 2023
What are the number systems in Computer?
Number systems are the technique to represent numbers in the computer system architecture, every value that you are saving or getting into/from computer memory has a defined number system.
Types of Computer Number Systems
Computer architecture supports following number systems.
- Binary number system
- Octal number system
- Decimal number system
- Hexadecimal (hex) number system
1) Binary Number System
A Binary number system has only two digits that are 0 and 1. Every number (value) represents with 0 and 1 in this number system. The base of binary number system is 2, because it has only two digits.
2) Octal number system
Octal number system has only eight (8) digits from 0 to 7. Every number (value) represents with 0,1,2,3,4,5,6 and 7 in this number system. The base of octal number system is 8, because it has only 8 digits.
3) Decimal number system
Decimal number system has only ten (10) digits from 0 to 9. Every number (value) represents with 0,1,2,3,4,5,6, 7,8 and 9 in this number system. The base of decimal number system is 10, because it has only 10 digits.
4) Hexadecimal number system
A Hexadecimal number system has sixteen (16) alphanumeric values from 0 to 9 and A to F. Every number (value) represents with 0,1,2,3,4,5,6, 7,8,9,A,B,C,D,E and F in this number system. The base of hexadecimal number system is 16, because it has 16 alphanumeric values. Here A is 10, B is 11, C is 12, D is 13, E is 14 and F is 15.
Table of the Numbers Systems with Base, Used Digits, Representation, C language representation:
| Number system |
Base |
Used digits |
Example |
C Language assignment |
| Binary |
2 |
0,1 |
(11110000)2 |
int val=0b11110000; |
| Octal |
8 |
0,1,2,3,4,5,6,7 |
(360)8 |
int val=0360; |
| Decimal |
10 |
0,1,2,3,4,5,6,7,8,9 |
(240)10 |
int val=240; |
| Hexadecimal |
16 |
0,1,2,3,4,5,6,7,8,9,
A,B,C,D,E,F |
(F0)16 |
int val=0xF0; |
Number System Conversions
The following are the types of number system conversions:
- Decimal Number System to Other Base
[for example: Decimal Number System to Binary Number System]
- Other Base to Decimal Number System
[for example: Binary Number System to Decimal Number System]
- Other Base to Other Base
[for example: Binary Number System to Hexadecimal Number System]
1. Decimal Number System to Other Base
To convert Number system from Decimal Number System to Any Other Base is quite easy; you have to follow just two steps:
- Divide the Number (Decimal Number) by the base of target base system (in which you want to convert the number: Binary (2), octal (8) and Hexadecimal (16)).
- Write the remainder from step 1 as a Least Signification Bit (LSB) to Step last as a Most Significant Bit (MSB).
| Decimal to Binary Conversion |
Result |
Decimal Number is : (12345)10
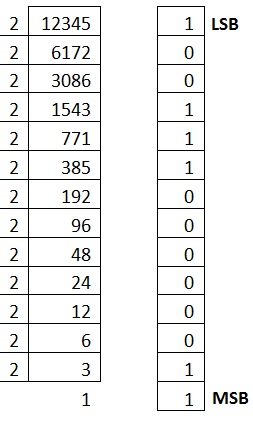
|
Binary Number is
(11000000111001)2
|
| Decimal to Octal Conversion |
Result |
Decimal Number is : (12345)10
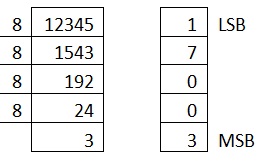
|
Octal Number is
(30071)8
|
| Decimal to Hexadecimal Conversion |
Result |
Example 1
Decimal Number is : (12345)10
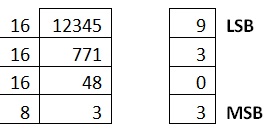
|
Hexadecimal Number is
(3039)16
|
Example 2
Decimal Number is : (725)10
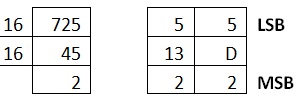
|
Hexadecimal Number is
(2D5)16
Convert
10, 11, 12, 13, 14, 15
to its equivalent...
A, B, C, D, E, F
|
2. Other Base System to Decimal Number Base
To convert a Number System from Any Other Base System to a Decimal Number System, you have to follow just three steps:
- Determine the base value of the source Number System (that you want to convert), and also determine the position of digits from LSB (first digit’s position – 0, second digit's position – 1, and so on).
- Multiply each digit with its corresponding multiplication of position value and Base of Source Number System's Base.
- Add the resulting value in step B.
Below given examples contain the following rows:
- Row 1 contains the DIGITs of the number (that is going to be converted).
- Row 2 contains the POSITION of each digit in the number system.
- Row 3 contains the multiplication: DIGIT* BASE^POSITION.
- Row 4 contains the calculated result of step C.
- And then add each value of step D, resulted value is the Decimal Number.
| Binary to Decimal Conversion |
Binary Number is : (11000000111001)2
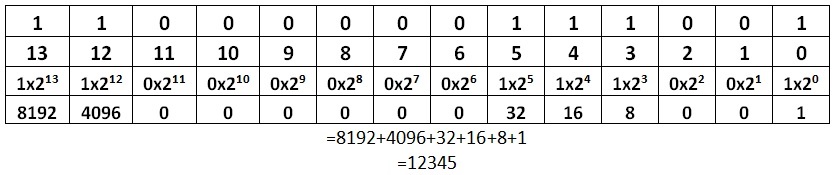
|
| Octal to Decimal Conversion |
Result |
Octal Number is : (30071)8
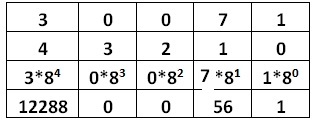
|
=12288+0+0+56+1
=12345
Decimal Number is: (12345)10
|
| Hexadecimal to Decimal Conversion |
Result |
Hexadecimal Number is : (2D5)16
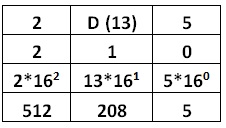
|
=512+208+5
=725
Decimal Number is: (725)10
|
Advertisement
Advertisement