Home » Digital Electronics

Octal to Binary, Decimal, and Hexadecimal Number Systems Conversion

In this tutorial, we will learn about the conversion of octal to binary, decimal, and hexadecimal number systems with the help of examples. By Saurabh Gupta Last updated : May 10, 2023

1. Octal to Binary Number System Conversion

To convert octal numbers into binary numbers, we can use the relationship between octal and binary numbers.

Octal Number	Binary Number
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

Example 1: Convert (73.2)₈ into ( ? )₂

Solution

Using the table provided above, we can replace octal numbers with their equivalent binary digits.

    7 = 111
    3 = 011
    2 = 010

Therefore, (73.2)₈ = (111 011.010)₂

Example 2: Convert (475.62)₈ into ( ? )₂

Solution

Using the table provided above, we can replace octal numbers with their equivalent binary digits.

    4 = 100
    7 = 111
    5 = 101
    6 = 110
    2 = 010

Therefore, (475.62)₈ = (100 111 101.110 010)₂

2. Octal to Decimal Number System Conversion

Conversion of octal number into a decimal number can be done using the positional weights by multiplying the positional weights with the corresponding bit and add them all together to obtain the decimal number.

• In an integral part of the octal number, the weights follow the pattern as 8⁰, 8¹, 8², 8³, 8⁴, 8⁵ and so on from right to left.
• In the fractional part of the octal number, the weights follow the pattern as 8^-1, 8^-2, 8^-3, 8^-4, 8^-5 and so on from left to right.

Example 1: Convert (75.3)₈ = ( ? )₁₀

Solution

We multiply each bit with the corresponding positional weight and then add them together to get the result.

Therefore, (75.3)₈ = (61.375)₁₀

Example 2: Convert (624.712)₈ = ( ? )₁₀

Solution

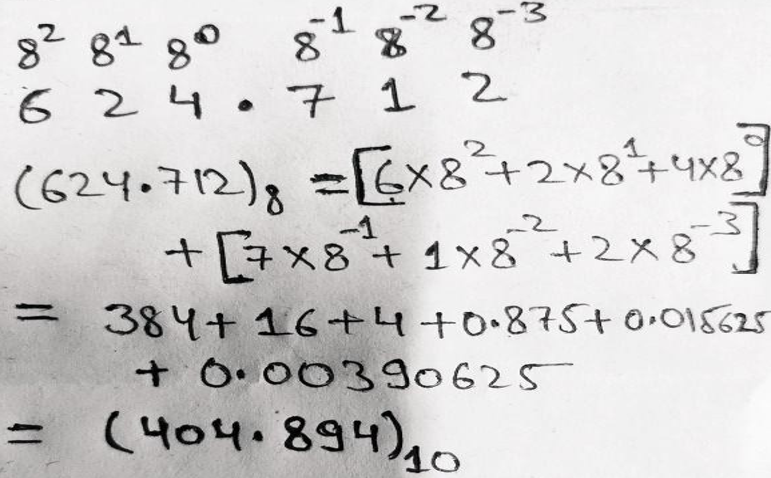
We multiply each bit with the corresponding positional weight and then add them together to get the result.

Therefore, (624.712)₈ = (404.894)₁₀

Example 3: Convert (482.31)₈ = ( ? )₁₀

Solution

Given number (482.31)₈ is not an octal number as a range of octal number is from 0 to 7 and the given number includes 8. So, it cannot be converted to a decimal number.

3. Octal to Hexadecimal Number System Conversion

Conversion of the octal number to hexadecimal can only be done using a certain definite path. We first have to convert octal number to binary number and then convert the binary number into hexadecimal number i.e., Octal Number → Binary Number → Hexadecimal Number

Example 1: Convert (35.7)₈ into ( ? )₁₆

Solution

Step 1: Convert octal number to binary number.
Therefore, (35.7)₈ = (011101.111)₂

Step 2: Convert binary number to a hexadecimal number.
Therefore, (011101.111)₂ = (1D.E)₁₆

Therefore, (35.7)₈ = (1D.E)₁₆

Note: To know how to convert the binary number into a hexadecimal number?, Read: Conversion of binary number into a hexadecimal number.

Example 2: Convert (73.2)₈ into ( ? )₁₆

Solution

Step 1: Convert octal number to binary number.
Therefore, (73.2)₈ = (111011.010)₂

Step 2: Convert binary number to a hexadecimal number.
Therefore, (111011.010)₂ = (3B.4)₁₆

Therefore, (73.2)₈ = (3B.4)₁₆

---