Home »
Digital Electronics
Binary to Hexadecimal Number System Conversion
In this tutorial, we will learn about the conversion of binary to hexadecimal number systems with the help of examples.
By Saurabh Gupta Last updated : May 10, 2023
Prerequisite: Number systems
Binary to Hexadecimal Number System Conversion
Converting binary numbers into hexadecimal numbers is similar to the conversion of binary into octal, it just requires some modifications. The relationship between binary numbers and hexadecimal numbers is given as:
| Decimal | Hexadecimal | Binary |
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| 10 | A | 1010 |
| 11 | B | 1011 |
| 12 | C | 1100 |
| 13 | D | 1101 |
| 14 | E | 1110 |
| 15 | F | 1111 |
In hexadecimal number system, we have sixteen digits ranging from 0 to 15 which can be represented using four-bit binary numbers in 24 = 16 ways, so starting from the least significant bit of the binary number, we group four successive bits of the binary number to get its equivalent hexadecimal number as seen from the table above.
In an integral part, the grouping of four bits is done from the right side to the left side whereas in the fractional part the grouping of four bits is done from left to right and then convert it to its equivalent hexadecimal symbol.
In the process of grouping four bits, one/two/three bits can be added to the left of the MSB in an integral part and/or to the right of the LSB bit of the fractional part of the binary number.
Note: Whenever we need any additional bits, we only add '0' as the additional bit.
Example 1: Convert (01111111.1010)2 to ( ? )16
Solution
We will make a grouping of 4 bits from right to left direction in an integral part and from left to right direction in the fractional part and then replace it with the corresponding symbol with the help of the table provided above.
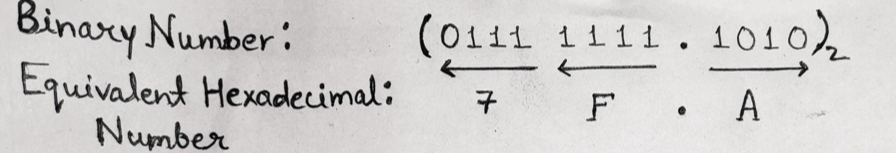
Therefore, (01111111.1010)2 = (7F. A)16
Example 2: Convert (1110011100.110001)2 to ( ? )16
Solution
The given binary number consists of only 10 bits in an integral part and only 6 bits in the fractional part. So, making a group of 4 bits is not possible. In this case, we have to add bits from our side so that we can make a grouping of 4 bits. Thus, we add two zero bits at the LHS of the MSB in the integral part which will make 12 bits in an integral part, without disturbing its original value. Similarly, two zero bits are added to the RHS of the LSB in the fractional part, which will result in 8 bits in the fractional part and can be grouped in a group of 4 bits.
Thus, above given binary number can now be written as: (001110011100.11000100)2
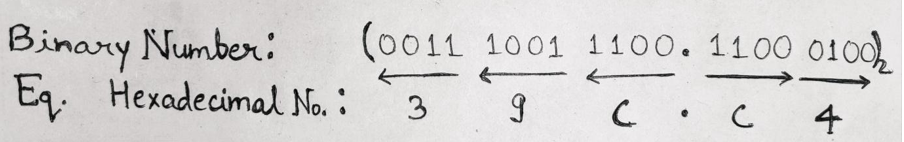
Therefore, (001110011100.11000100)2 = (39C.C4)16
Example 3: Convert (100101011110.0110111)2 to ( ? )16
Solution
Given binary number has 12 bits in an integral part, so it can be easily grouped in a group of 4 bits but there are only 7 bits in the fractional part so we need to add one more additional zero bit to the RHS of LSB in the fractional part. Thus, the above binary number can now be written as: (100101011110.01101110)2
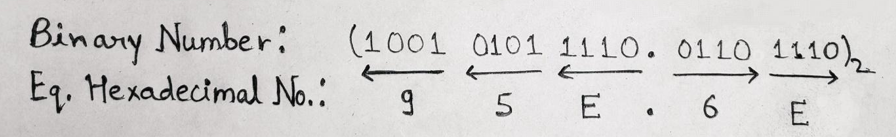
Therefore, (100101011110.01101110)2 = (95E.6E)16
Advertisement
Advertisement