Home » Digital Electronics

Binary Coded Decimal (BCD Code) and Its Addition

In this tutorial, we will learn about the binary-coded decimal (BCD code) and its addition (binary-coded decimal addition) with the help of examples. By Saurabh Gupta Last updated : May 10, 2023

Prerequisite: Number systems

Binary Coded Decimal (BCD Code)

BCD Code (8421 Code): In BCD 8421 code, each decimal digit is represented using a 4-bit binary number. The 4-bit binary numbers have their weights attached as 8, 4, 2, 1 from MSB to LSB side. Since the weights are attached to it comes in the category of weighted codes and is also sequential.

In a digital system that accepts only binary numbers in form of 0 and 1, the only way to interpret decimal numbers is its conversion from decimal to binary and vice-versa which is a slow process and it also requires a huge electronic circuitry. So, we use BCD numbers. Also, the sequential nature of BCD numbers makes it advantageous for performing arithmetic operations.

Although, there are many advantages there are some disadvantages too such as:

BCD codes are more inefficient than usual binary codes. Usually, in binary numbers, we represent (13)₁₀ = (1101)₂ i.e., we require 4-bits but in BCD notation (13)₁₀ is represented as (0001 0011). Here, we require 8-bits to represent the same 13.

Another disadvantage is that arithmetic operations become more complex as compared to the usual binary numbers because, in BCD numbers, we have 6 illegal states as 1010, 1011, 1100, 1101, 1110 and 1111 which are not part of 8421 BCD system.

Relation Between Decimal, Binary, and 8421 BCD Numbers

The following table describes the relation between Decimal, Binary and 8421 BCD numbers.

Decimal Numbers	Binary Numbers	8421 BCD Numbers
0	0000	0000
1	0001	0001
2	0010	0010
3	0011	0011
4	0100	0100
5	0101	0101
6	0110	0110
7	0111	0111
8	1000	1000
9	1001	1001
10	1010	0001 0000
11	1011	0001 0001
12	1100	0001 0010
13	1101	0001 0011
14	1110	0001 0100
15	1111	0001 0101
...	...	...
...	...	...
...	...	...

Example 1: Represent (28)₁₀ and (53)₁₀ in 8421 BCD notation

Solution

(28)₁₀ in BCD notation can be represented as (0010 1000).

Similarly, (53)₁₀ in BCD notation can be represented as (0101 0011).

Binary Coded Decimal Addition (BCD Addition)

The addition of BCD numbers is slightly different from binary addition. Here, the rules of binary addition are partially applicable only to the individual 4-bit groups. The BCD addition, is thus carried out by individually adding the corresponding 4-bit groups starting from the LSB side and if there is a carry to the next group, or if the result belongs to any of the 6 illegal states than we add 6₁₀(0110) to the sum term of that group and resulting carry is added in the next group.

Example: Perform BCD Addition of 6 and 7

Solution

BCD representation of 6 is given as 0110 and for 7 it is 0111.

When we add 6 and 7 in BCD, we get 1101 which is an invalid state therefore, we add 0110 (6) to the sum to get correct result which is 0001 0011 (13).

Example 2: Perform BCD Addition of 8765 and 3943

Solution

BCD representation of 8765 is given as 1000 0111 0110 0011 and for 3943 it is 0011 1001 0100 0011.

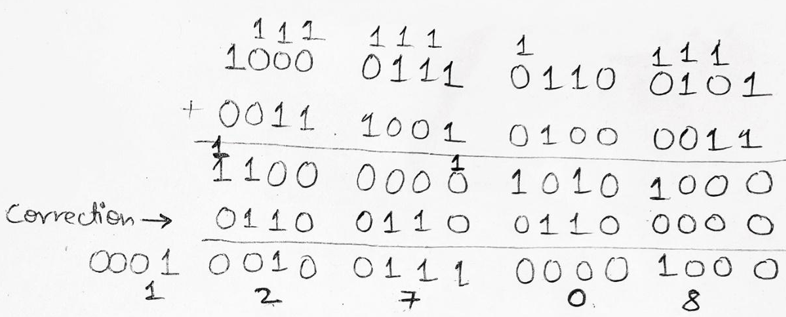
Firstly, we will perform a normal binary addition of two numbers now we see 1100 and 1010 which are illegal states also the third group of 4-bits from LSB side i.e., 0000 has a carry 1 to the next group. So, for correction, we have to add 0110 to all three groups. Thus, we get the correct result as 0001 0010 0111 0000 1000 which is equivalent to (12708)₁₀ in decimal number system and this is what we get on adding (8765)₁₀ + (3943)₁₀ = (12708)₁₀. Hence, our result is also verified.

---