Home »
Digital Electronics
Representation of Number Systems
In this tutorial, we will learn how to represent the various number systems with the help of examples.
By Saurabh Gupta Last updated : May 10, 2023
Any number system has a set of symbols known as Digits with some rules performing arithmetic operations. A collection of these makes a number has two parts. They are integer portion and fraction portion. These portions are separated by a point known as radix.
Number Systems Representation
If a number has radix as 'b', then the number of numbers present in that number system will be 'b' which will range from 0 to b-1.
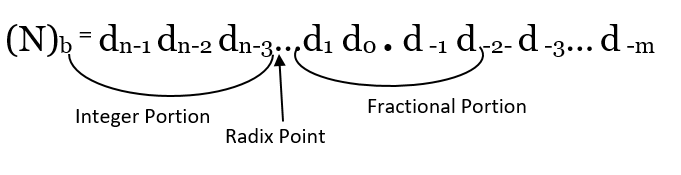
Where,
- N = a number
- b = radix or base to number system
- n = number of digits in integer portion
- m = number of digits in the fractional portion
- dn-1 = Most Significant Digit (MSD)
- d-m = Least Significant Digit (LSD)
Types of Number System Representation
The following are the representation of various number systems:
- Binary Number System Representation
- Octal Number System Representation
- Decimal Number System Representation
- Hexadecimal Number System Representation
1. Binary Number System Representation
The binary number system has its base as 2. Since b=2, it consists of two digits which range from 0 to 2-1 =1. (As discussed above, the range is from 0 to b-1).
Therefore, the binary number system consists of digits 0 and 1 only.
Ex: (1101)2, (110101)2, (0101)2, (101.01)2, etc.
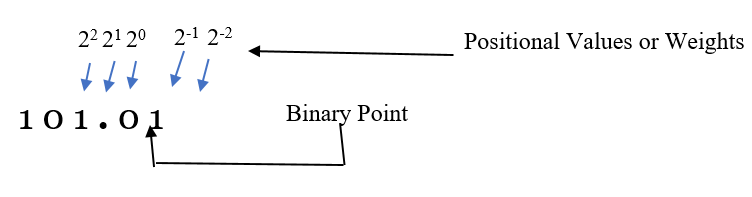
In Binary Number System, the portion to the left of binary point (integer part) have their weights as 20, 21, 22 and so on from right to left. The portion on the right-hand side of the binary point (fractional part) have weights as 2-1, 2-2 and so on from left to right.
Above given binary number (101.01)2 can be represented as:
(101.01)2 = (1*22) + (0*21) + (1*20) + (0*2-1) + (1*2-2)
After simplifying the terms in the RHS of the equation, we will get a decimal number equivalent to binary number on the LHS which is (5.25)10.
2. Octal Number System Representation
The octal number system has its base as 8. Since b=8, it consists of eight digits which range from 0 to 8-1 =7. (As discussed above, the range is from 0 to b-1).
It consists of digits ranging from 0 to 7 i.e., 0, 1, 2, 3, 4, 5, 6 and 7.
Ex: (73)8, (420)8, (125.13)8, etc.
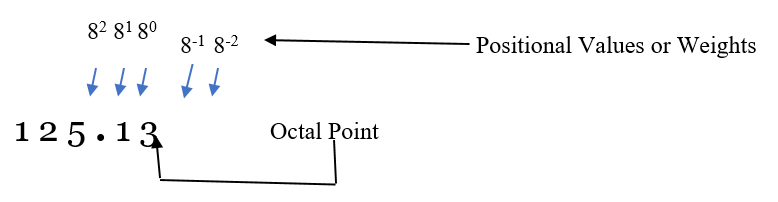
In Octal Number System the positional values/weights to the left of octal point in integer part are as 80, 81, 82 and so on from right to left whereas the weights in the right-hand side in fractional part are as 8-1, 8-2 and so on from left to right.
Above given octal number (125.13)8 can be represented as:
(125.13)8 = (1*82) + (2*81) + (5*80) + (1*8-1) + (3*8-2)
After simplifying the terms in the RHS of the equation, we will get a decimal number equivalent to octal number on the LHS which is (85.140625)10.
3. Decimal Number System Representation
The Decimal Number System has its base as 10. Since b=10, it consists of 10 digits which range from 0 to 10-1 = 9. (As discussed above, the range is from 0 to b-1).
It consists of digits ranging from 0 to 9 i.e., 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
Ex: (101)10, (12)10, (999)10, (540.25)10, etc.
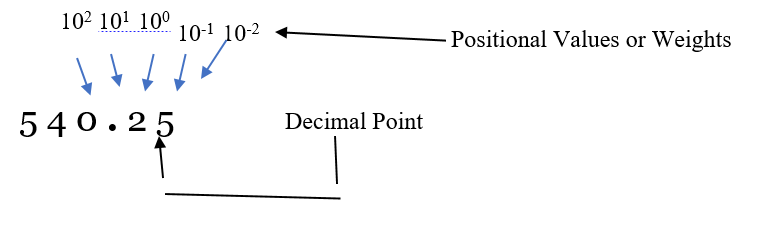
In the Decimal Number System the positional values/weights to the left of the decimal point in integer part are as 100, 101, 102 and so on from right to left whereas the weights in the right-hand side in fractional part are as 10-1, 10-2 and so on from left to right.
Above given decimal number (540.25)10 can be represented as:
(540.25)10 = (5*102) + (4*101) + (0*100) + (2*10-1) + (5*10-2)
After simplifying the terms in the RHS of the equation, we will get a decimal number equivalent to the decimal number on the LHS.
4. Hexadecimal Number System Representation
The Hexadecimal Number System has its base as 16. Since b=16, it consists of 16 digits which range from 0 to 16-1 = 15. (As discussed above, the range is from 0 to b-1).
It consists of both digits and alphabets where digits range from 0 to 9 i.e., 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 and alphabets range from A to F where (A=10), (B=11), (C=12), (D=13), (E=14) and (F=15).
Ex: (123)16, (459)16, (12A3F.12)16, etc.
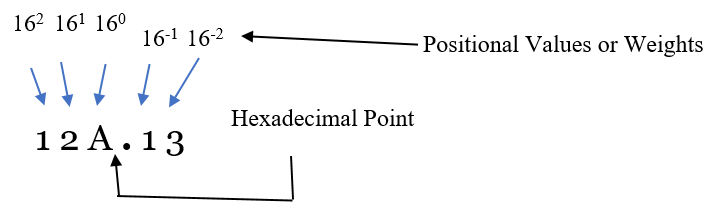
In the Hexadecimal Number System the positional values/weights to the left of the decimal point in integer part are as 160, 161, 162 and so on from right to left whereas the weights in the right-hand side in fractional part are as 16-1, 16-2 and so on from left to right.
Above given Hexadecimal number (12A.13)16 can be represented as:
(12A.13)16 = (1*162) + (2*161) + (10*160) + (1*16-1) + (3*16-2)
After simplifying the terms in the RHS of the equation, we will get a decimal number equivalent to decimal number on the LHS which is (298. 06640625)10.
Advertisement
Advertisement