Home »
Digital Electronics
Binary Addition and Subtraction with Examples
In this tutorial, we will learn about the binary addition and subtraction with the help of examples.
By Saurabh Gupta Last updated : May 10, 2023
1) Binary Addition
Since binary numbers consist of only two digits 0 and 1, so their addition is different from decimal addition. Addition of binary numbers can be done following certain rules:
| A | B | Sum | Carry |
|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
The above table contains two bits a and b, their sum and carry.
On adding,
0 + 0 = 0,
0 + 1 = 1,
1 + 0 = 1,
1 + 1 = 10 (i.e., sum is 0 and carry is 1)
Let's do some exercise and solution some questions based on binary addition to get more of the topic.
Example 1: Perform (10)2 + (11)2
Solution
Using the rules provided above, sum operation can be performed as:
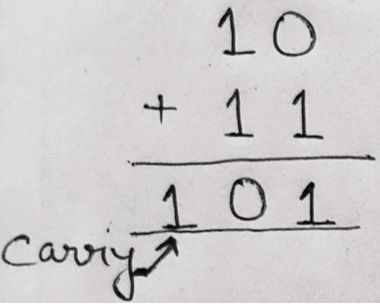
Therefore, (10)2 + (11)2 = (101)2
Verification:
We can verify our result by converting the above binary numbers into decimal numbers and then verifying the sum.
Here, (10)2 = (2)10, (11)2 = (3)2 and (101)2 = (5)10, thus when we will add 2 and 3 we get sum as 5.
Example 2: Perform (1)2 + (1)2 + (1)2 + (1)2
Solution
Using the rules provided above, sum operation can be performed as:
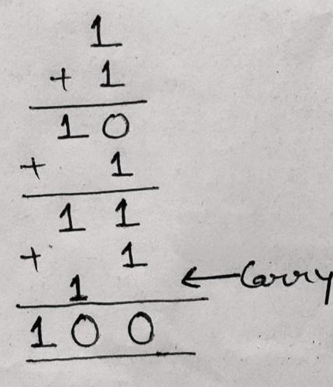
Example 3: Perform (110)2 + (111)2 + (101)2
Solution
Using the rules provided above, sum operation can be performed as:
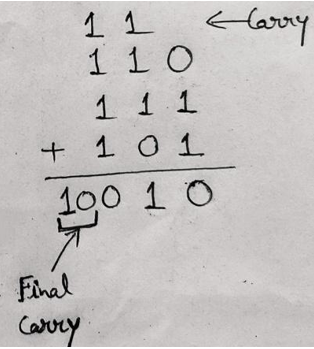
Verification:
We can verify our result as (110)2=(6)10, (111)2=(7)10, (101)2= (5)10 and (10010)2= (18)10. So when we will add 6 + 7 + 5 =18, which we are getting as our answer.
2) Binary Subtraction
The binary subtraction is performed like decimal subtraction, the rules for binary subtraction are:
| A | B | Difference | Borrow |
|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Example 1: Subtract (10)2 from (1001)2
Solution
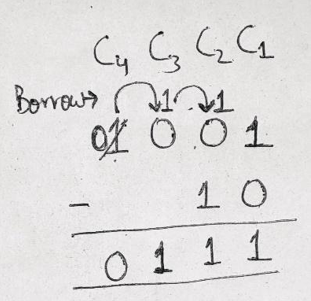
In column C2, 1 can't be subtracted from 0 so, we have to borrow 1 from column C3, but C3 also has a 0, so 1 must be borrowed from column C4, the 1 borrowed from column C4 becomes 10 in column C3, now keeping 1 in column C3 bringing the remaining 1 to column C2 which becomes 10 in column C2 thus 10 – 1= 1 in column C2.
In column C3, 1 – 0 = 1
In column C4, 1 after providing borrow 1 is reduced to 0.
Therefore, (1001)2 – (10)2 = (111)2
Example 2: Subtract (111.111)2 from (1010.01)2
Solution

In Column C0, 1 can't be subtracted from 0, so we have to borrow 1 from column C1, which becomes 10 in column C0, thus 10 – 1 = 1,
In column C1, after providing borrow 1 to C0, C1 is reduced to 0. Now 1 can't be subtracted from so borrow 1 from C2, but it is also 0, so borrow 1 from C3 which is also 0, so borrow 1 from C4, reducing column C4 to 0. Now, this 1 borrowed from column C4 becomes 10 in column C3, keep 1 in the column C3 and bring other 1 to column C2, which makes column C2 as 10 now again bring 1 from C2 to C1, which reduces C2 to 1 and makes C1 as 10.
Thus, In Column C1, 10 – 1 = 1
In Column C2, 1 – 1 = 0
In Column C3, 1 – 1 = 0
In Column C4, we now have 1 to be subtracted from 0 which is not possible so we will borrow 1 from Column C5, but Column C5 has a 0 so borrow 1 from C6 making C6 to be 0 and bring it to C5 which makes it 10 in C5, keep 1 in C5 and bring the other 1 to C4 which makes C4 as 10 thus
In column C4, 10 – 1 = 1
In column C5, 1 – 1 = 0
In column C6, 0 – 0 = 0
Hence, the result is (1010.01)2 – (111.111)2 = (0010.011)2
Advertisement
Advertisement