Home » Data Structure

Shortest path between two nodes in graph using Djikstra algorithm

This article will tell you what is graph, nodes, shortest distance and how to find it by Djikstra algorithm? By Manu Jemini, on January 06, 2018

What is a Graph?

Graph is a set of nodes or known number of vertices. When these vertices are paired together, we call it edges. An Edge is a line from one node to other. Every edge can have its cost or weight.

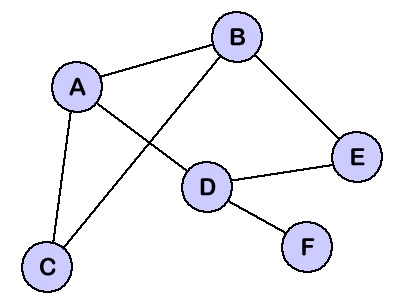
Image source: https://courses.cs.vt.edu/csonline/DataStructures/Lessons/Graphs/graph.gif

What is Node?

Node is a vertex in the graph at a position. The Line between two nodes is an edge. The Edge can have weight or cost associate with it.

Shortest

Shortest distance is the distance between two nodes. For Example, to reach a city from another, can have multiple paths with different number of costs. A path with the minimum possible cost is the shortest distance.

Djikstra Algorithm

Djikstra algorithm asks for the source and destination. The Algorithm finds the shortest distance from current node to the next node and then at the next node look for the cheapest path for the next node.

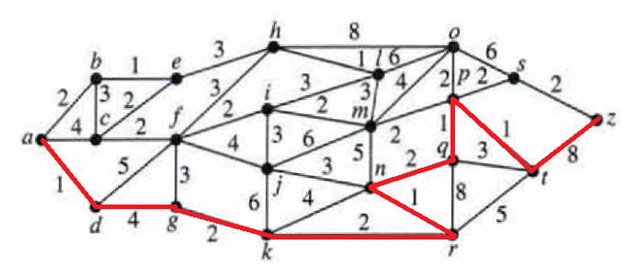
Image source https://i.stack.imgur.com/tyTz7.pngsrc

C program to find shortest path between two nodes in graph using Djikstra algorithm

#include<stdio.h>

#define MAX 10
#define TEMP 0
#define PERM 1
#define infinity 9999

struct node {
  int predecessor;
  int dist; /*minimum distance of node from source*/
  int status;
};

int adj[MAX][MAX];
int n;

void create_graph() {
  int i, max_edges, origin, destin, wt;

  printf("Enter number of vertices : ");
  scanf("%d", & n);
  max_edges = n * (n - 1);

  for (i = 1; i <= max_edges; i++) {
    printf("Enter edge %d(0 0 to quit) : ", i);
    scanf("%d %d", & origin, & destin);
    if ((origin == 0) && (destin == 0))
      break;
    printf("Enter weight for this edge : ");
    scanf("%d", & wt);
    if (origin > n || destin > n || origin <= 0 || destin <= 0) {
      printf("Invalid edge!\n");
      i--;
    } else
      adj[origin][destin] = wt;
  } /*End of for*/
} /*End of create_graph()*/

void display() {
  int i, j;
  for (i = 1; i <= n; i++) {
    for (j = 1; j <= n; j++)
      printf("%3d", adj[i][j]);
    printf("\n");
  }

} /*End of display()*/

int findpath(int s, int d, int path[MAX], int * sdist) {
  struct node state[MAX];
  int i, min, count = 0, current, newdist, u, v;
  * sdist = 0;
  /* Make all nodes temporary */
  for (i = 1; i <= n; i++) {
    state[i].predecessor = 0;
    state[i].dist = infinity;
    state[i].status = TEMP;
  }

  /*Source node should be permanent*/
  state[s].predecessor = 0;
  state[s].dist = 0;
  state[s].status = PERM;

  /*Starting from source node until destination is found*/
  current = s;
  while (current != d) {
    for (i = 1; i <= n; i++) {
      /*Checks for adjacent temporary nodes */
      if (adj[current][i] > 0 && state[i].status == TEMP) {
        newdist = state[current].dist + adj[current][i];
        /*Checks for Relabeling*/
        if (newdist < state[i].dist) {
          state[i].predecessor = current;
          state[i].dist = newdist;
        }
      }
    } /*End of for*/

    /*Search for temporary node with minimum distand make it current node*/
    min = infinity;
    current = 0;
    for (i = 1; i <= n; i++) {
      if (state[i].status == TEMP && state[i].dist < min) {
        min = state[i].dist;
        current = i;
      }
    } /*End of for*/

    if (current == 0) /*If Source or Sink node is isolated*/
      return 0;
    state[current].status = PERM;
  } /*End of while*/

  /* Getting full path in array from destination to source	*/
  while (current != 0) {
    count++;
    path[count] = current;
    current = state[current].predecessor;
  }

  /*Getting distance from source to destination*/
  for (i = count; i > 1; i--) {
    u = path[i];
    v = path[i - 1];
    * sdist += adj[u][v];
  }
  return (count);
} /*End of findpath()*/

int main() {
  int i, j;
  int source, dest;
  int path[MAX];
  int shortdist, count;

  create_graph();
  printf("The adjacency matrix is :\n");
  display();

  while (1) {
    printf("Enter source node(0 to quit) : ");
    scanf("%d", & source);
    printf("Enter destination node(0 to quit) : ");
    scanf("%d", & dest);

    if (source == 0 || dest == 0)
      return 1;
    count = findpath(source, dest, path, & shortdist);
    if (shortdist != 0) {
      printf("Shortest distance is : %d\n", shortdist);
      printf("Shortest Path is : ");
      for (i = count; i > 1; i--)
        printf("%d->", path[i]);
      printf("%d", path[i]);
      printf("\n");
    } else
      printf("There is no path from source to destination node\n");
  } /*End of while*/
  
  return 0;
} /*End of main()*/

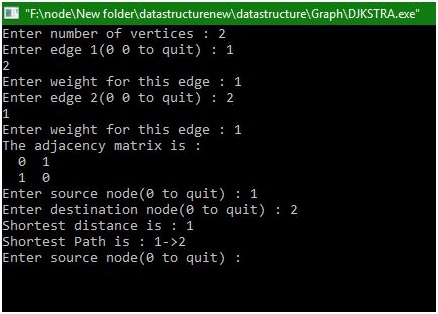
Output