Home » Computer Science Organization

Booth's Algorithm | Computer Science Organization

In this article, we are going to learn about Booths algorithm in computer system organization with its example and flowchart.
Submitted by Abhishek Kataria, on July 29, 2018

Booth's algorithm

This is a kind of algorithm which uses a more straightforward approach. This algorithm also has the benefit of the speeding up the multiplication process and it is very efficient too. Binary multiplication which has signed number uses this type of algorithms named as Booth's algorithm.

Flowchart of Booth's algorithm

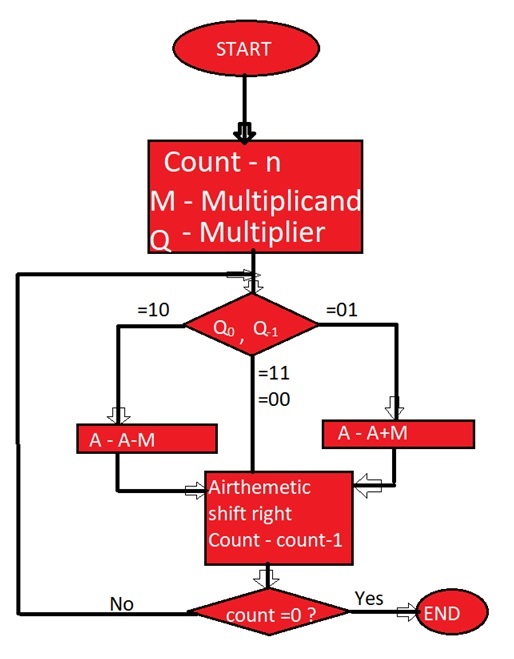
Booth’s algorithm for two complements multiplication:

1. Multiplier and multiplicand are placed in the Q and M register respectively.
2. Result for this will be stored in the AC and Q registers.
3. Initially, AC and Q_-1 register will be 0.
4. Multiplication of a number is done in a cycle.
5. A 1-bit register Q_-1 is placed right of the least significant bit Q₀ of the register Q.
6. In each of the cycle, Q₀ and Q_-1 bits will be checked.
   1. If Q₀ and Q_-1 are 11 or 00 then the bits of AC, Q and Q_-1 are shifted to the right by 1 bit.
   2. If the value is shown 01 then multiplicand is added to AC. After addition, AC, Q₀, Q_-1 register are shifted to the right by 1 bit.
   3. If the value is shown 10 then multiplicand is subtracted from AC. After subtraction AC, Q₀, Q_-1 register is shifted to the right by 1 bit.

Basically, Booth’s algorithm uses the concept of an arithmetic right shift in which the leftmost bit is not only shifted right by 1 bit but it also remains in the original position.

Example: Let us multiply (-6) and (2) using Booth’s algorithm.

Solution: (6)₁₀ = (0110)₂

As it is given multiplicand, M= (-6)₁₀ =2 complement of 0110 = 1010

Multiplier, Q= (2)₁₀ = 0010

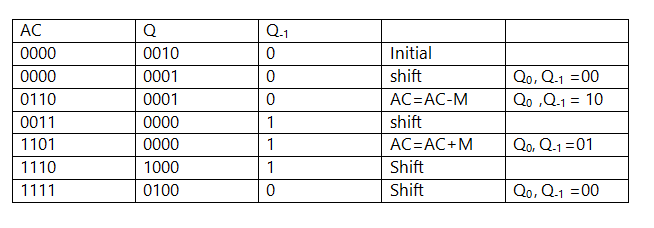
Product by Booth’s algorithm= 1111 0100