Home » DBMS

Precedence Graph | DBMS

DBMS Precedence Graph: In this tutorial, we will learn about the precedence graph and the algorithm for testing conflict serializability of a schedule in the database management system. By Anushree Goswami Last updated : May 31, 2023

Precedence Graph

A precedence graph, also known as serialization graph or conflict graph, is used for testing Conflict Serializability of a schedule in the condition that forms the setting of concurrency control in databases.

It is also known as a directed Graph G = (V, E), which consists of a pair of a set of nodes V = {V1, V2, V3, ..., Vn} and a set of directed edges E = {E1, E2, E3, ..., Em}. Where the set of nodes V are testing to retrieve identical data attribute through the transactions of a schedule and the set of edges E is regulated connectivity between a set of two nodes.

Nodes: In the graph, for each transaction Tp the graph contains a single node. So, In a schedule of a precedence graph, The total number of transactions will be similar to the total number of nodes.

Edges: An edge is regulated connectivity between a set of two distinct transactions Tq and Tr and it shows in the format Tq –>Tr, where Tq is the beginning of the edge and Tr is the ending.

The Algorithm for testing Conflict Serializability of a schedule

1. Create a node T, for each transaction participating in schedule S in the precedence graph.
2. For every condition in schedule S create an edge Tp → Tq in the precedence graph if a Transaction Tq implements a read_item (Z) after Tp implements a write_item (Z). It's a Read-Write conflict.
3. For every condition in schedule S create an edge Tp → Tq in the precedence graph if a Transaction Tq implements a write_item (Z) after Ti implements a read_item (Z). It's a Write-Read conflict.
4. For every condition in schedule S create an edge Tp → Tq in the precedence graph If a Transaction Tq implements a write_item (Z) after Tp implements a write_item (Z). It's a Write-Write conflict.
5. If and only if there is no cycle in the precedence graph, then the schedule S is Serializable.

Example:

Q1) Find the following Schedule S is conflict Serializable or not?

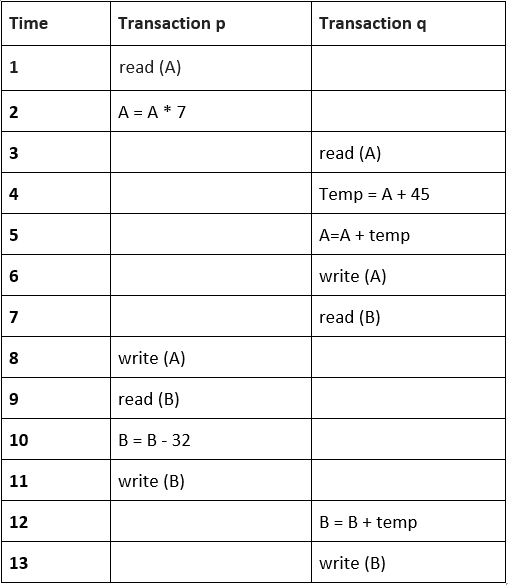
Solution:

Let's make a precedence graph,

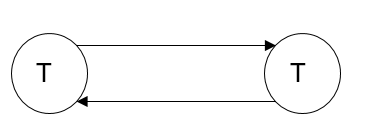
In the above precedence graph, by following accordingly to the Algorithm, Transaction Tp implements reads A before Transaction Tq implements writes A, therefore the first arrow directed from Transaction Tp towards Transaction Tq and Transaction Tq reads B before Transaction Tp writes B, therefore the second arrow directed from Transaction Tq towards Transaction Tp.

Since from the above precedence graph it's clearly visible that the graph is cyclic, therefore the schedule S is not conflicted Serializable.

Q2) Find the following Schedule S is conflict Serializable or not?

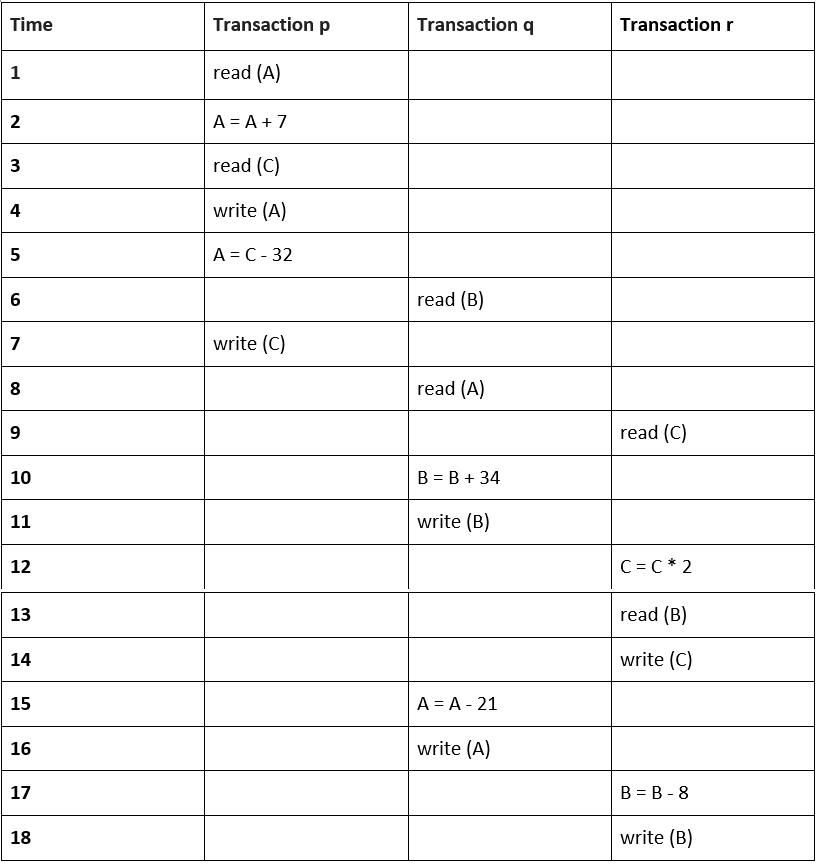
Solution:

Let's make a precedence graph,

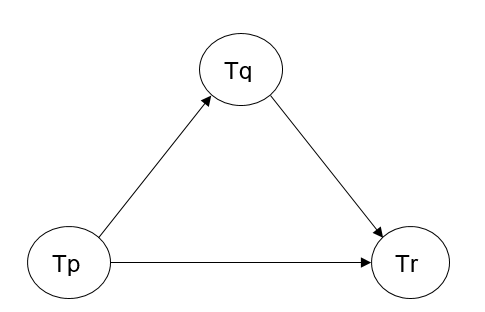
In the above precedence graph, by following accordingly to the Algorithm, Transaction Tp implements reads A before Transaction Tq implements writes A, therefore the first arrow directed.

from Transaction Tp towards Transaction Tq and Transaction Tq reads B before Transaction Tr writes B, therefore the second arrow directed from Transaction Tq towards Transaction Tr and then the Transaction Tp reads C before Transaction Tr writes C, therefore the third arrow directed from Transaction Tp towards Tr.

Since from the above precedence graph it's clearly visible that the graph is acyclic, therefore the schedule S is conflict Serializable.