Home » DBMS

Equivalence of Functional Dependencies in DBMS

In this tutorial, we will learn about the equivalence of functional dependencies in database management system with the help of examples. By Pratishtha Saxena Last updated : May 31, 2023

What is Equivalence of Functional Dependencies in DBMS?

In the context of databases, functional dependency is a relationship between two sets of attributes within a database table. It describes the dependency of one set of attributes, known as the dependent attributes, on another set of attributes, known as the determinant attributes.

In other words, a functional dependency indicates that the values of certain attributes (dependent attributes) are determined by the values of another set of attributes (determinant attributes) within the same table.

Formally, in a relation or table schema R, a functional dependency is represented as follows:

A -> B

Here, A and B are sets of attributes within the table. This notation indicates that for any two tuples (rows) t1 and t2 in R, if the values of attributes in A are equal for t1 and t2, then the values of attributes in B must also be equal for t1 and t2.

Functional dependencies play a crucial role in database design, normalization, and ensuring data integrity. They help to identify and eliminate redundant data and provide a basis for organizing tables and defining relationships. Functional dependencies can be used to determine candidate keys, which are minimal sets of attributes that uniquely identify a tuple in a relation.

What is Equivalent Set of Functional Dependencies?

An equivalent set of functional dependencies refers to a collection of functional dependencies that expresses the same set of relationships among attributes within a database table. It means that two sets of functional dependencies are equivalent if they imply the same set of constraints and can be used interchangeably to describe the dependencies within a table.

Formally, two sets of functional dependencies F1 and F2 are equivalent if:

• F1 implies every functional dependency in F2, and
• F2 implies every functional dependency in F1.

In other words, if F1 and F2 are equivalent, they convey the same information about the relationships between attributes in the table. They can be used interchangeably to represent the dependencies and constraints within the database schema.

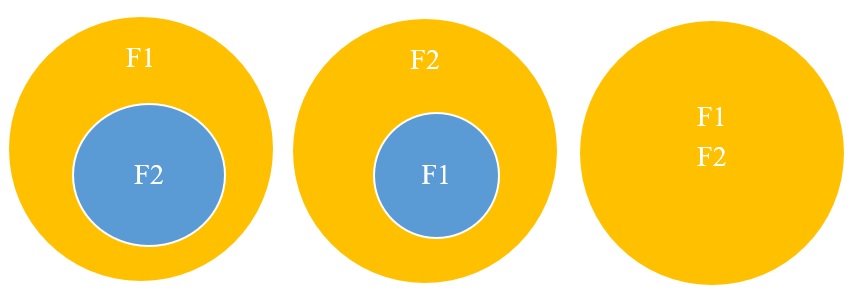
Determining the equivalent set of functional dependencies is essential in database design and normalization. It helps to ensure that the dependencies are properly represented and that the table schema is free from redundancy and data anomalies. Equivalent sets of functional dependencies provide different representations of the same information and allow for flexibility in expressing the relationships between attributes in a concise and efficient manner.

Steps to check the equivalence of two different sets of functional dependencies

To check the equivalence of two different sets of functional dependencies, you can follow these steps:

• Step 1: Convert both sets of functional dependencies into canonical form.
• Step 2: Check if each functional dependency in one set is implied by the other set.
• Step 3: Check if each functional dependency in the second set is implied by the first set.

If both sets pass these steps and all dependencies in each set are implied by the other set, then the two sets of functional dependencies are equivalent.

Advantages of Functional Dependencies

1. Data Integrity: Functional dependencies help maintain data integrity by ensuring that the relationships between attributes are properly defined and enforced.
2. Redundancy Reduction: Functional dependencies allow for the identification and elimination of redundant data. By organizing data based on functional dependencies, you can avoid storing the same information in multiple places.
3. Database Design: Functional dependencies play a crucial role in the process of database design and normalization. They help in decomposing complex tables into smaller, well-structured tables, improving data organization, and reducing data duplication.
4. Query Optimization: Understanding the dependencies between attributes can help the query optimizer make informed decisions about query execution plans, resulting in improved query performance.

Disadvantages of Functional Dependencies

1. Complexity: Managing and analysing functional dependencies can be complex, especially in large databases with numerous tables and dependencies.
2. Dependency Maintenance: As the database evolves over time, functional dependencies may need to be updated or modified to reflect changes in the data model or application requirements.
3. Overhead: Applying functional dependencies can introduce some overhead in terms of storage and performance.
4. Limited Expressiveness: Functional dependencies have limitations in expressing complex relationships and dependencies that go beyond simple attribute-to-attribute relationships.

Functional dependencies provide a foundation for data integrity and efficient database design, but they also require careful consideration and management to ensure their effectiveness.

Example based on Equivalence of Functional Dependencies

Q) A relation R (P, Q, U, S, and T) is having two functional dependencies sets R1 and R2, which is shown as

Set R1:         Set R2:
P → C           P → QU
PQ → U          S → PT
S → T

Solution...

Case 1) Determining Whether R2 ⊃ R1 or not

Step 1)

• (P)+ = {P, Q, U} // closure of left side of P → QU using set R1.
• (S)+ = {P, Q, U, S, T} // closure of left side of S → PT using set R1.

Step 2)

• (P)+ = {P, Q, U} // closure of left side of P → QU using set R2.
• (S)+ = {P, Q, U, S, T} // closure of left side of S → PT using set R2.

Step 3)

Comparing the results of Step 1 and Step 2, we find,

• Functional dependencies of set R2 can determine all the attributes which have been determined by the functional dependencies of set R1.
• Thus, we conclude R2 is a subset of R1 i.e. R2 ⊃ R1.

Case 2) Determining Whether R1 ⊃ R2 or not

Step 1)

• (P)⁺ = {P, Q, U} // closure of left side of P→ Q using set R2.
• (PQ)⁺ = {P, Q, U} // closure of left side of PQ → U using set R2.
• (S)⁺ = {P, Q, U, S, T} // closure of left side of S → PU and S → T using set R2.

Step 2)

• (P)⁺ = {P, Q, U} // closure of left side of P→ Q using set R1.
• (PQ)⁺ = {P, Q, U} // closure of left side of PQ → U using set R1.
• (S)⁺ = {P, Q, U, S, T} // closure of left side of S → PU and S → T using set R1.

Step 3)

Comparing the results of Step 1 and Step 2, we find,

• Functional dependencies of set R1 can determine all the attributes which have been determined by the functional dependencies of set R2.
• Thus, we conclude R1 is a subset of R2 i.e. R1 ⊃ R2.

Case 3) Determining Whether Both R1 and R2 satisfy each other or not

• From Step 1, we conclude R2 ⊃ R1.
• From Step 2, we conclude R1 ⊃ R2.
• Thus, we conclude that both R1 and R2 satisfied each other i.e. R1 = R2.