Home » Kotlin

Program for Heapsort in Kotlin

In this article, we are going to learn how to implement Heapsort in Kotlin? Here you will find what is Heapsort, its algorithm, and program in Kotlin.
Submitted by Aman Gautam, on December 17, 2017

Quicksort is a sorting algorithm which uses binary heap data structure. A heap is a data structure that we can see as an almost / complete binary tree in which each node act as an element. Heaps can max heap or min heap. In the max heap, the root element is greater than its children while in min heap, the root is smaller than its children.

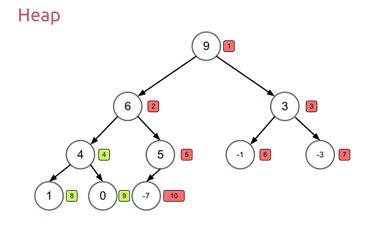
Image from http://www.stoimen.com/

The algorithm starts with building a max heap, then swap the root (max element) with the last element, then applying heapify to the remaining heap except for the last one as it is already in its position. This will decrease the length of the heap by one. Repeat the step until all the elements get their position.

Heap sort sorts given elements in O(nlog(n)) time in all cases. This is a little bit difficult to implement than other O(nlogn) time sorting algorithm i.e. quick sort and merge sort as we have to manage a special data structure i.e. heap.

Algorithms

    MAX_HEAPIFY(A.i)
    1.	l = left(i)
    2.	 r = right(i);
    3.	if ((l <= heapSize- 1) && (A[l] > A[i])) 
    4.	largest = l
    5.	else
    6.	largest = i
    7.	if ((r <= heapSize- 1) && (A[r] >A[l]))
    8.	    largest = r
    9.	if (largest != i) 
    10.	swap(A, i, largest)
    11.	max_heapify(A, largest)

    BUILD_MAX_HEAP(A)
    1.	A.heapsize=A.length
    2.	for i =heapSize/ 2 downTo0 
    3.	max_heapify(A, i)

    HEAP_SORT(A)
    1.	build_Max_heap(A)
    2.	for i =A.size- 1 downTo1) 
    3.	swap(A, i, 0)
    4.	heapSize= heapSize–1
    5.	max_heapify(A, 0)

Algorithm source from Introduction to Algorithms by cormen

Program to implement Heapsort in Kotlin

var heapSize = 0

fun left(i: Int): Int {
    return 2 * i
}

fun right(i: Int): Int {
    return 2 * i + 1
}

fun swap(A: Array<Int>, i: Int, j: Int) {
    var temp = A[i]
    A[i] = A[j]
    A[j] = temp
}

fun max_heapify(A: Array<Int>, i: Int) {
    var l = left(i);
    var r = right(i);
    var largest: Int;

    if ((l <= heapSize - 1) && (A[l] > A[i])) {
        largest = l;
    } else
        largest = i

    if ((r <= heapSize - 1) && (A[r] > A[l])) {
        largest = r
    }

    if (largest != i) {
        swap(A, i, largest);
        max_heapify(A, largest);
    }
}

fun buildMaxheap(A: Array<Int>) {
    heapSize = A.size
    for (i in heapSize / 2 downTo 0) {
        max_heapify(A, i)
    }
}

fun heap_sort(A: Array<Int>) {
    buildMaxheap(A)
    for (i in A.size - 1 downTo 1) {
        swap(A, i, 0)
        heapSize = heapSize - 1
        max_heapify(A, 0)

    }
}

fun main(arg: Array<String>) {
    print("Enter no. of elements :")
    var n = readLine()!!.toInt()

    println("Enter elements : ")
    var A = Array(n, { 0 })
    for (i in 0 until n)
        A[i] = readLine()!!.toInt()

    heap_sort(A)

    println("Sorted array is : ")
    for (i in 0 until n)
        print("${A[i]}  ")
}

Output

Enter no. of elements :5
Enter elements :
12
23
44
54
1
Sorted array is :
1  12  23  44  54