Home » Python

Perceptron algorithm and its implementation in Python

Python | Perceptron algorithm: In this tutorial, we are going to learn about the perceptron learning and its implementation in Python.
Submitted by Anuj Singh, on July 04, 2020

Perceptron Algorithm is a classification machine learning algorithm used to linearly classify the given data in two parts. It could be a line in 2D or a plane in 3D. It was firstly introduced in the 1950s and since then it is one of the most popular algorithms for binary classification. Mathematically, it is the simplest algorithm and also has an application in Deep Learning.

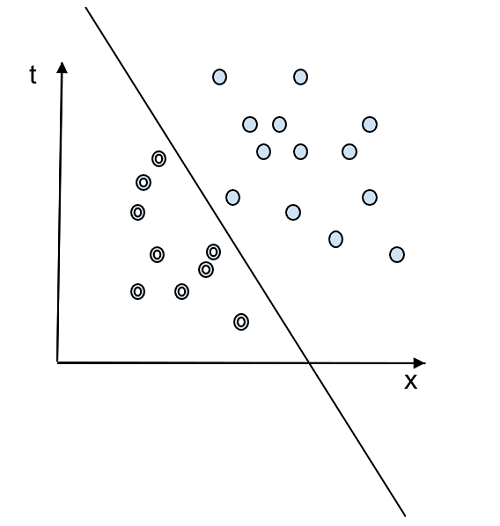
This figure shows that data can be classified into two classes by a line. Therefore, this is a linearly separable and perceptron algorithm that can be used for classification. In machine learning language, this line is called the decision boundary. It is defined as: f( θ.x + θ₀) = 0

The algorithm is based on this decision boundary as it separates the plane into two regions such that:

f(θ⋅ x + θ₀) > 0, for positively labelled data and
f(θ⋅ x + θ₀) < 0, for negatively labelled datapoint.

If the given dataset is linearly separable, then there must exist a linear classifier  such that y⁽ⁱ ⁾ (θ⋅ x⁽ⁱ ⁾ + θ₀) > 0 satisfying all data points x⁽ⁱ⁾, where y⁽ⁱ ⁾ is the label.

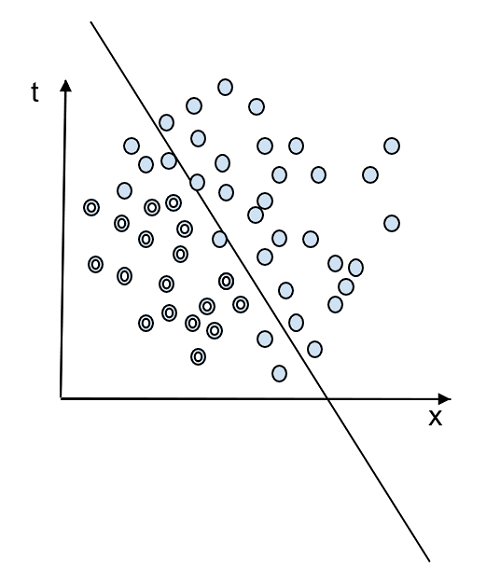
The figure 2 shows a case when the data is not linearly separable and there cannot exist a linear classifier θ.x + θ₀ = 0 such that y⁽ⁱ⁾ (θ⋅ x⁽ⁱ⁾ + θ₀) > 0 satisfying all data points x⁽ⁱ⁾, where y⁽ⁱ⁾ is the label. The Perceptron algorithm can be used only for binary classification and it is the simplest one.

Note: If the classifier passes through the origin, i.e. no offset then the value θ₀= 0.
f( θ.x ) = 0

Algorithm:

Initialization 
𝛳 = 0, a vector
𝛳0 = 0, a scalar

Iterate 1,2,3 .... T
	Iterate through data points i = 1,2,3 .... n
		if Y(i).(𝛳.X(i) + 𝛳0) <= 0
			𝛳 = 𝛳 + Y(i).X(i)
			𝛳0 = 𝛳0 + Y(i)
Return 𝛳, 𝛳0

Note: Sometime, when all the points are not linearly separable but applying perceptron will result in a classification with some error or can be said as Loss.

Loss function:

When the linear classifier classifies data points with some points negative classified i.e. y⁽ⁱ⁾ (θ⋅ x⁽ⁱ⁾ + θ₀) <= 0 (for points i <= n), then the simplest loss function can be defined as the number of negatively classified points. In other words, the number of i in the above expression is called a loss function.

Note: The loss function can be further modified but this is the simplest one and it does not take into account the error magnitude (i.e. distance of a miss classified point from the classifier).

Python Function for Perceptron Algorithm

# Machine Learning
# Perceptron Algorithm Pyhton function

import numpy as np

def perceptron_single_step_update(
        feature_vector,
        label,
        current_theta,
        current_theta_0):

    theta = current_theta
    theta_0 = current_theta_0
    if label*(np.matmul(current_theta, feature_vector) + current_theta_0) <= 0:
        theta = theta + label*feature_vector
        theta_0 = theta_0 + label
    
    return (theta, theta_0)   

def perceptron(feature_matrix, labels, T):    
    [m,n] = np.shape(feature_matrix)
    tt = np.zeros(n)
    tt_0 = 0
    
    for t in range(T):
        for i in range(m):
            vec = feature_matrix[i]
            (tt, tt_0) = perceptron_single_step_update(vec, labels[i], tt, tt_0)
    return (tt, tt_0)