Home »
C programming language
Infix To Postfix Conversion Using Stack [with C program]
Infix to Postfix Conversion in C: In this tutorial, we will learn how to convert Infix to Postfix using stack with the help of C program?
By Abhishek Jain Last updated : April 13, 2023
Overview
One of the applications of Stack is in the conversion of arithmetic expressions in high-level programming languages into machine readable form. As our computer system can only understand and work on a binary language, it assumes that an arithmetic operation can take place in two operands only e.g., A+B, C*D,D/A etc. But in our usual form an arithmetic expression may consist of more than one operator and two operands e.g. (A+B)*C(D/(J+D)).
These complex arithmetic operations can be converted into polish notation using stacks which then can be executed in two operands and an operator form.
What is an Infix Expression?
It follows the scheme of <operand><operator><operand> i.e. an <operator> is preceded and succeeded by an <operand>. Such an expression is termed infix expression. E.g., A+B
What is a Postfix Expression?
It follows the scheme of <operand><operand><operator> i.e. an <operator> is succeeded by both the <operand>. E.g., AB+
Algorithm to Convert Infix to Postfix Expression
The following are the steps (algorithm) to convert an infix expression to a postfix expression:
- Let, X is an arithmetic expression written in infix notation.
- Push "("onto Stack, and add ")" to the end of X.
- Scan X from left to right and repeat Step 3 to 6 for each element of X until the Stack is empty.
- If an operand is encountered, add it to Y.
- If a left parenthesis is encountered, push it onto Stack.
-
If an operator is encountered ,then:
- Repeatedly pop from Stack and add to Y each operator (on the top of Stack) which has the same precedence as or higher precedence than operator.
- Add operator to Stack.
[End of If]
-
If a right parenthesis is encountered ,then:
- Repeatedly pop from Stack and add to Y each operator (on the top of Stack) until a left parenthesis is encountered.
- Remove the left Parenthesis.
[End of If]
[End of If]
- END.
Example of Infix to Postfix Conversion
Let's take an example to better understand the algorithm
Infix Expression: A+(B*C-(D/E^F)*G)*H, where ^ is an exponential operator.
Step by step output for infix to postfix conversion
| Input String | Output Stack | Operator Stack |
|---|
| A+(B*C-(D/E^F)*G)*H | | |
| A+(B*C-(D/E^F)*G)*H | A | |
| A+(B*C-(D/E^F)*G)*H | A | + |
| A+(B*C-(D/E^F)*G)*H | A | +( |
| A+(B*C-(D/E^F)*G)*H | AB | +( |
| A+(B*C-(D/E^F)*G)*H | AB | +(* |
| A+(B*C-(D/E^F)*G)*H | ABC | +(* |
| A+(B*C-(D/E^F)*G)*H | ABC* | +(- |
| A+(B*C-(D/E^F)*G)*H | ABC* | +(-( |
| A+(B*C-(D/E^F)*G)*H | ABC*D | +(-( |
| A+(B*C-(D/E^F)*G)*H | ABC*D | +(-(/ |
| A+(B*C-(D/E^F)*G)*H | ABC*DE | +(-(/ |
| A+(B*C-(D/E^F)*G)*H | ABC*DE | +(-(/^ |
| A+(B*C-(D/E^F)*G)*H | ABC*DEF | +(-(/^ |
| A+(B*C-(D/E^F)*G)*H | ABC*DEF^/ | +(- |
| A+(B*C-(D/E^F)*G)*H | ABC*DEF^/ | +(-* |
| A+(B*C-(D/E^F)*G)*H | ABC*DEF^/G | +(-* |
| A+(B*C-(D/E^F)*G)*H | ABC*DEF^/G*- | + |
| A+(B*C-(D/E^F)*G)*H | ABC*DEF^/G*- | +* |
| A+(B*C-(D/E^F)*G)*H | ABC*DEF^/G*-H | +* |
| A+(B*C-(D/E^F)*G)*H | ABC*DEF^/G*-H*+ | |
Advantage of Postfix Expression over Infix Expression
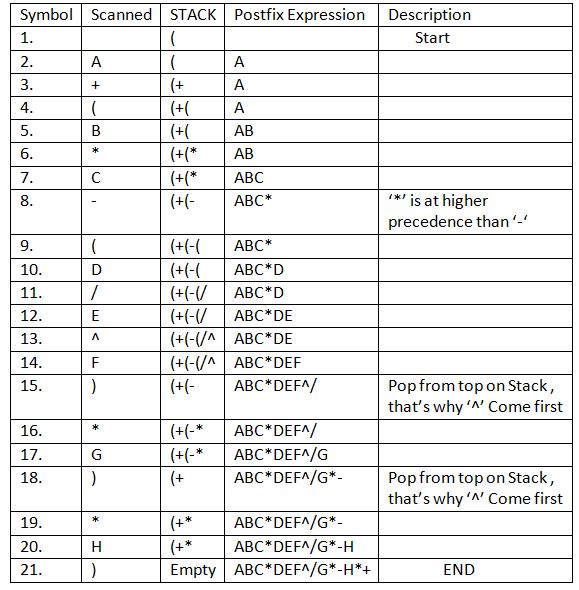
Resultant Postfix Expression: ABC*DEF^/G*-H*+
Advantage of Postfix Expression over Infix Expression
An infix expression is difficult for the machine to know and keep track of precedence of operators. On the other hand, a postfix expression itself determines the precedence of operators (as the placement of operators in a postfix expression depends upon its precedence).Therefore, for the machine it is easier to carry out a postfix expression than an infix expression.
C Program to Convert Infix to Postfix Expression
/* This program converts infix expression to postfix expression.
* This program assume that there are Five operators: (*, /, +, -,^)
in infix expression and operands can be of single-digit only.
* This program will not work for fractional numbers.
* Further this program does not check whether infix expression is
valid or not in terms of number of operators and operands.*/
#include <stdio.h>
#include <stdlib.h> /* for exit() */
#include <ctype.h> /* for isdigit(char ) */
#include <string.h>
#define SIZE 100
/* declared here as global variable because stack[]
* is used by more than one fucntions */
char stack[SIZE];
int top = -1;
/* define push operation */
void push(char item)
{
if (top >= SIZE - 1) {
printf("\nStack Overflow.");
}
else {
top = top + 1;
stack[top] = item;
}
}
/* define pop operation */
char pop()
{
char item;
if (top < 0) {
printf("stack under flow: invalid infix expression");
getchar();
/* underflow may occur for invalid expression */
/* where ( and ) are not matched */
exit(1);
}
else {
item = stack[top];
top = top - 1;
return (item);
}
}
/* define function that is used to determine whether any symbol is operator or not
(that is symbol is operand)
* this fucntion returns 1 if symbol is opreator else return 0 */
int is_operator(char symbol)
{
if (symbol == '^' || symbol == '*' || symbol == '/' || symbol == '+' || symbol == '-') {
return 1;
}
else {
return 0;
}
}
/* define fucntion that is used to assign precendence to operator.
* Here ^ denotes exponent operator.
* In this fucntion we assume that higher integer value
* means higher precendence */
int precedence(char symbol)
{
if (symbol == '^') /* exponent operator, highest precedence*/
{
return (3);
}
else if (symbol == '*' || symbol == '/') {
return (2);
}
else if (symbol == '+' || symbol == '-') /* lowest precedence */
{
return (1);
}
else {
return (0);
}
}
void InfixToPostfix(char infix_exp[], char postfix_exp[])
{
int i, j;
char item;
char x;
push('('); /* push '(' onto stack */
strcat(infix_exp, ")"); /* add ')' to infix expression */
i = 0;
j = 0;
item = infix_exp[i]; /* initialize before loop*/
while (item != '\0') /* run loop till end of infix expression */
{
if (item == '(') {
push(item);
}
else if (isdigit(item) || isalpha(item)) {
postfix_exp[j] = item; /* add operand symbol to postfix expr */
j++;
}
else if (is_operator(item) == 1) /* means symbol is operator */
{
x = pop();
while (is_operator(x) == 1 && precedence(x) >= precedence(item)) {
postfix_exp[j] = x; /* so pop all higher precendence operator and */
j++;
x = pop(); /* add them to postfix expresion */
}
push(x);
/* because just above while loop will terminate we have
oppped one extra item
for which condition fails and loop terminates, so that one*/
push(item); /* push current oprerator symbol onto stack */
}
else if (item == ')') /* if current symbol is ')' then */
{
x = pop(); /* pop and keep popping until */
while (x != '(') /* '(' encounterd */
{
postfix_exp[j] = x;
j++;
x = pop();
}
}
else { /* if current symbol is neither operand not '(' nor ')' and nor
operator */
printf("\nInvalid infix Expression.\n"); /* the it is illegeal symbol */
getchar();
exit(1);
}
i++;
item = infix_exp[i]; /* go to next symbol of infix expression */
} /* while loop ends here */
if (top > 0) {
printf("\nInvalid infix Expression.\n"); /* the it is illegeal symbol */
getchar();
exit(1);
}
if (top > 0) {
printf("\nInvalid infix Expression.\n"); /* the it is illegeal symbol */
getchar();
exit(1);
}
postfix_exp[j] = '\0'; /* add sentinel else puts() fucntion */
/* will print entire postfix[] array upto SIZE */
}
/* main function begins */
int main()
{
char infix[SIZE], postfix[SIZE]; /* declare infix string and postfix string */
/* why we asked the user to enter infix expression
* in parentheses ( )
* What changes are required in porgram to
* get rid of this restriction since it is not
* in algorithm
* */
printf("ASSUMPTION: The infix expression contains single letter variables and single digit constants only.\n");
printf("\nEnter Infix expression : ");
gets(infix);
InfixToPostfix(infix, postfix); /* call to convert */
printf("Postfix Expression: ");
puts(postfix); /* print postfix expression */
return 0;
}
Output
First Run:
Enter Infix expression : A+(B*C-(D/E^F)*G)*H
Postfix Expression: ABC*DEF^/G*-H*+
Second Run:
Enter Infix expression : (3^2*5)/(3*2-3)+5
Postfix Expression: 32^5*32*3-/5+
Advertisement
Advertisement