Home »
Computer Network
Transmission Impairment: What It Is, Consequences, and Causes
Computer Network | Transmission Impairment: In this tutorial, we will learn about the transmission impairment, its consequences, and causes of impairment.
By Monika Jha Last updated : May 05, 2023
Transmission Impairment
In the data communication system, analog and digital signals go through the transmission medium. Transmission media are not ideal. There are some imperfections in transmission mediums. So, the signals sent through the transmission medium are also not perfect. This imperfection cause signal impairment.
It means that signals that are transmitted at the beginning of the medium are not the same as the signals that are received at the end of the medium that is what is sent is not what is received. These impairments tend to deteriorate the quality of analog and digital signals.
Consequences
- For a digital signal, there may occur bit errors.
- For analog signals, these impairments degrade the quality of the signals.
Causes of Impairment
There are three main causes of impairment are,
- Attenuation
- Distortion
- Noise
1. Attenuation
Here attenuation Means loss of energy that is the weaker signal. Whenever a signal transmitted through a medium it loses its energy, so that it can overcome by the resistance of the medium.
- That is why a wire carrying electrical signals gets warm, if not hot, after a while. Some of the electrical energy is converted to heat in the signal.
- Amplifiers are used to amplify the signals to compensate for this loss.
- This figure shows the effect of attenuation and amplification:
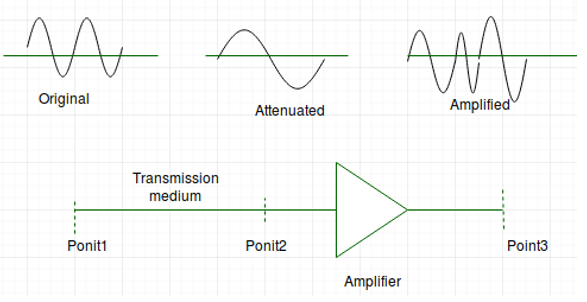
- A signal has lost or gained its strength, for this purpose engineers use the concept of decibel(dB).
- Decibel is used to measure the relative strengths of two signals or a signal at two different points.
- If a signal is attenuated then dB is negative and if a signal is amplified so the db is positive.
Attenuation(dB) = 10log10(P2/P1)
where P2 and P1 are the power of a signal at points1 and 2.
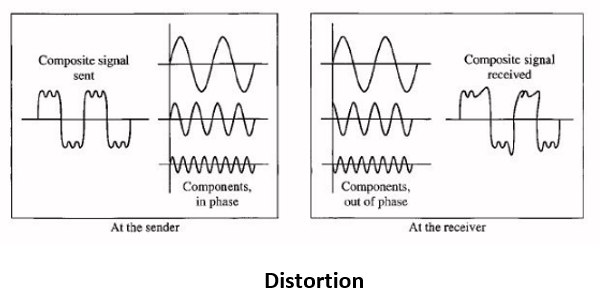
2. Distortion
If a signal changes its form or shape, it is referred to as distortion. Signals made up of different frequencies are composite signals. Distortion occurs in these composite signals.
- Each component of frequency has its propagation speed traveling through a medium and therefore, different components have different delay in arriving at the final destination.
- It means that signals have different phases at the receiver than they did at the source.
- This figure shows the effect of distortion on a composite signal:
3. Noise
Noise is another problem. There are some random or unwanted signals mix up with the original signal is called noise. Noises can corrupt the signals in many ways along with the distortion introduced by the transmission media.

Different types of noises are:
- Thermal noise
- Intermodulation noise
- Crosstalk
- Impulse noise
a) Thermal noise
The thermal noise is random motion of electrons in a conductor that creates an extra signal not originally sent by the transmitter.
It is also known as white noise because it is distributed across the entire spectrum (as the frequency encompass over a broad range of frequencies).
b) Intermodulation noise
More than one signal share a single transmission channel, intermodulation noise is generated.
For instance, two signals S1 and S2 will generate signals of frequencies (S1 + S2) and (s1 - S2), which may interfere with the signals of the same frequencies sent by the sender. due to If nonlinearity present in any part of the communication system, intermodulation noise is introduced.
c) Cross talk
Cross talk is an effect a wire on the another. One wire acts as a sending antenna and the transmission medium acts as the receiving antenna.
Just like in telephone system, it is a common experience to hear conversation of other people in the background. This is known as cross talk.
d) Impulse noise
Impulse noise is irregular pulses or spikes( a signal with high energy in a very short period) generated by phenomena like that comes from power lines, lightning, spark due to loose contact in electric circuits and so on.
It is a primary source of bit-errors in digital data communication that kind of noise introduces burst errors.
Advertisement
Advertisement