Home » C++ programming language

Dijkstra's Algorithm: Explanation and Implementation with C++ program

Dijkstra's Algorithm: In this tutorial, we will learn about Dijkstra's algorithm, why it is used, and the implementation of Dijkstra's algorithm with the help of a C++ program. By Shubham Singh Rajawat Last updated : August 06, 2023

Dijkstra's Algorithm

Dijkstra's algorithm aka the shortest path algorithm is used to find the shortest path in a graph that covers all the vertices.

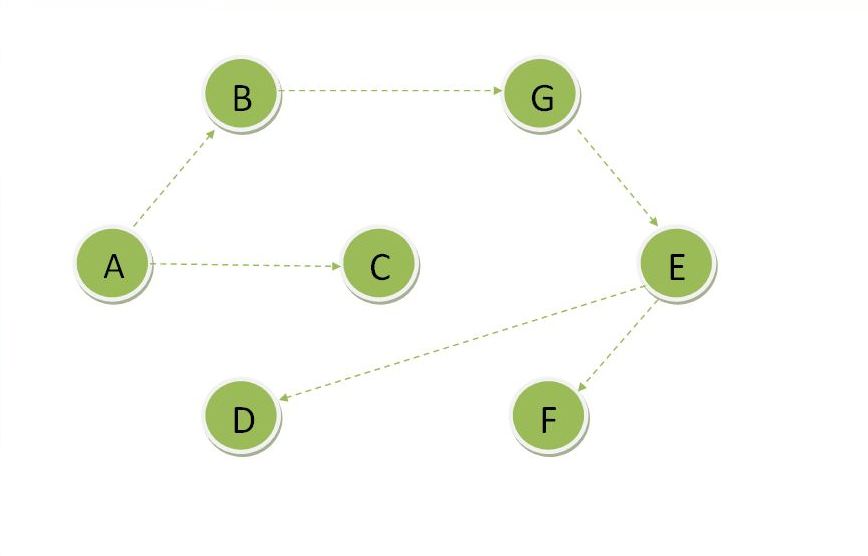
Given a graph with the starting vertex.

Dijkstra's Algorithm Implementation Steps

The steps to implement Dijkstra's algorithm are:

• Initially Dset contains src: dist[s]=0 dist[v]= ∞
• Set Dset to initially empty
• While all the elements in the graph are not added to 'Dset'

  A. Let 'u' be any vertex not in 'Dset' and has minimum label    dist[u]
  B. Add 'u' to Dset
  C. Update the label of the elements adjacent to u
      For each vertex 'v' adjacent to u
        If 'v' is not in 'Dset' then 
          If dist[u]+weight(u,v)<dist[v] then
  	      Dist[v]=dist[u]+weight(u,v)

Dijkstra's Algorithm Example with Explanation

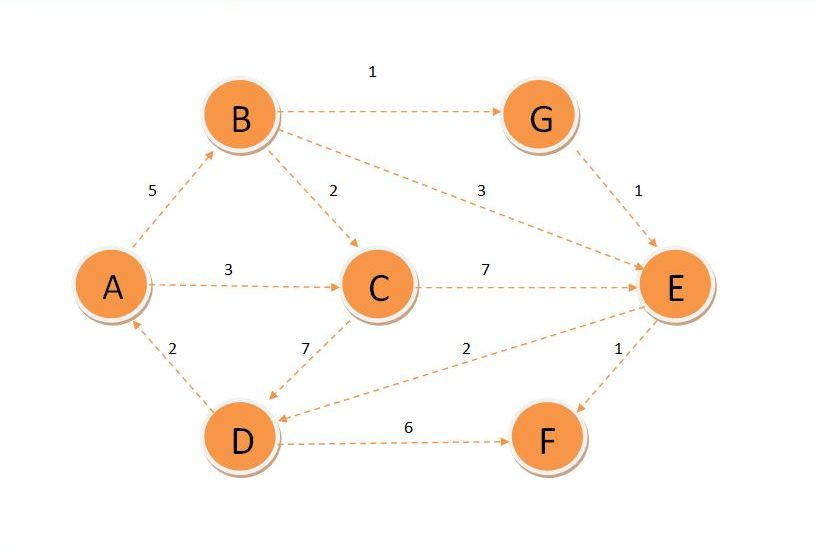
Let us understand this with the help of an example:

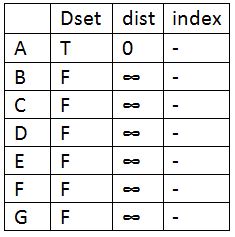
Initially Dset is empty and the distance of all the vertices is set to infinity except the source which is set to zero. First we find the vertex with minimum distance. The vertex ‘A’ got picked as it is the source so update Dset for A.

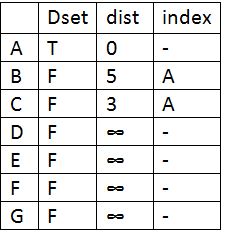
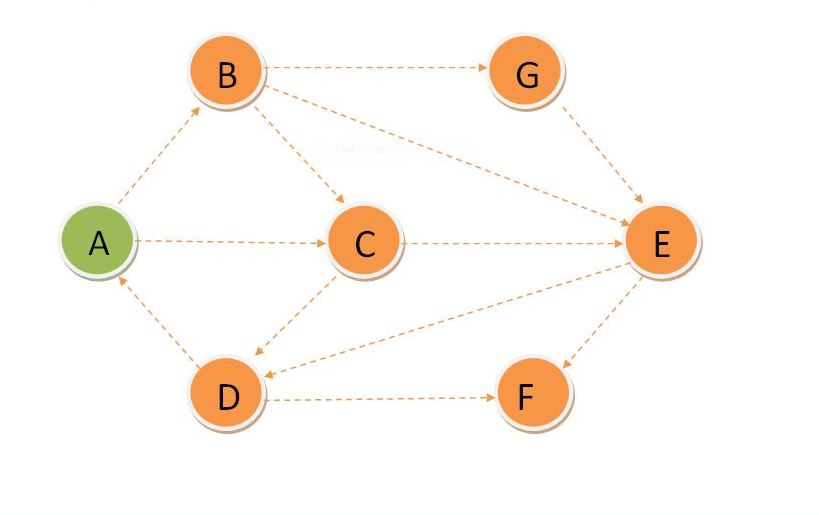
Now update the distance of its adjacent vertices which B and C. Now find the vertex whose distance is minimum which is C.

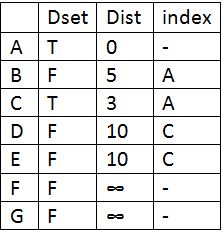
So update Dset for C and update the distance of its adjacent vertices. Find the vertex with minimum distance which is B.

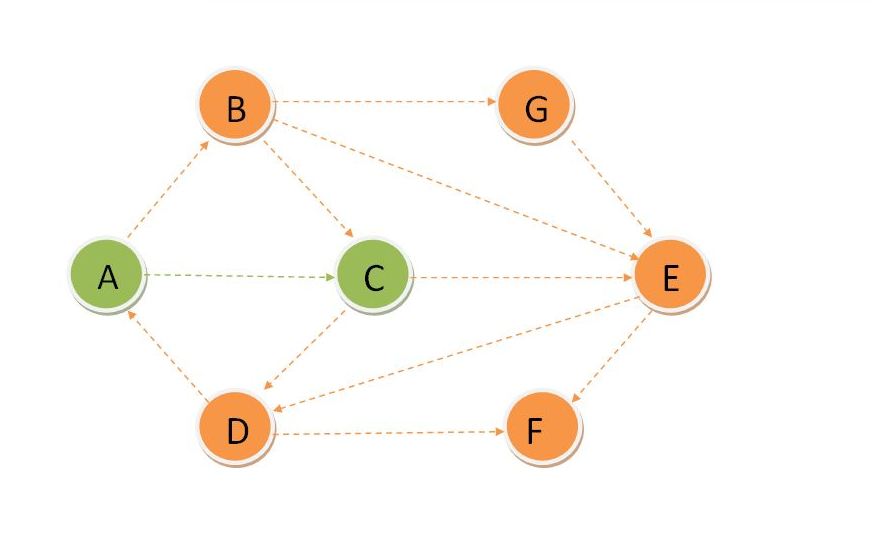
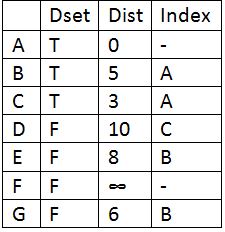
Update Dset for B and update distance of its adjacent vertices and then find the vertex with minimum distance which is G.

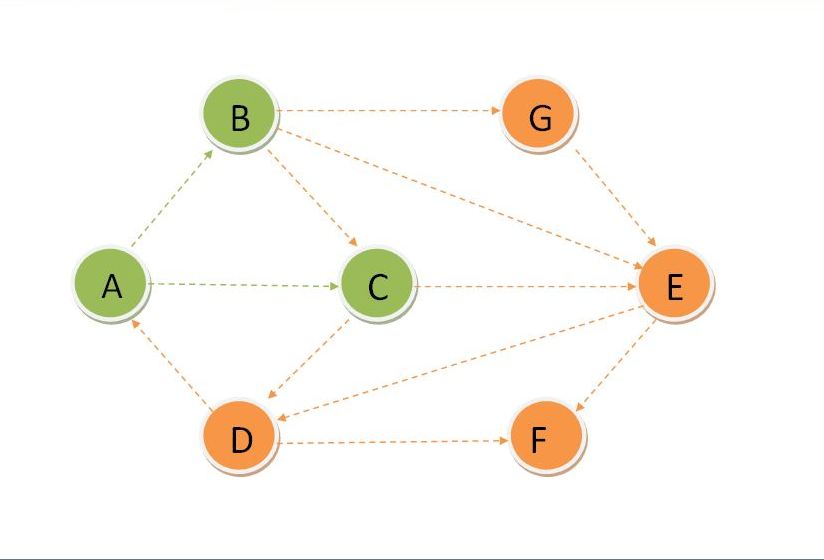
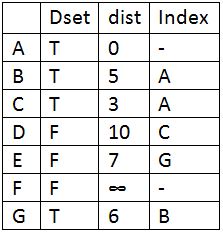
Update Dset for G and update distance of its adjacent vertices and find the vertex with minimum distance which is E.

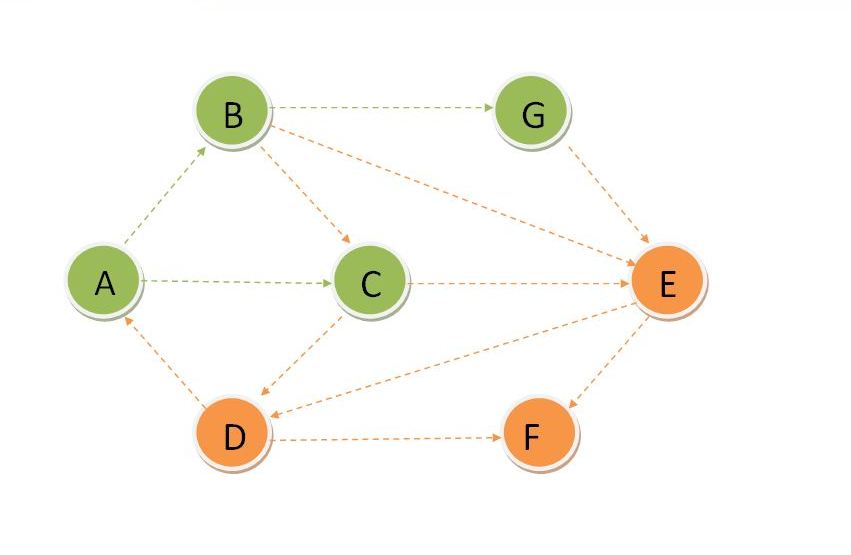
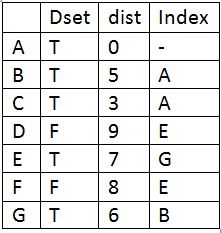
Update Dset for E and update distance of its adjacent vertices and find the vertex with minimum distance which is F.

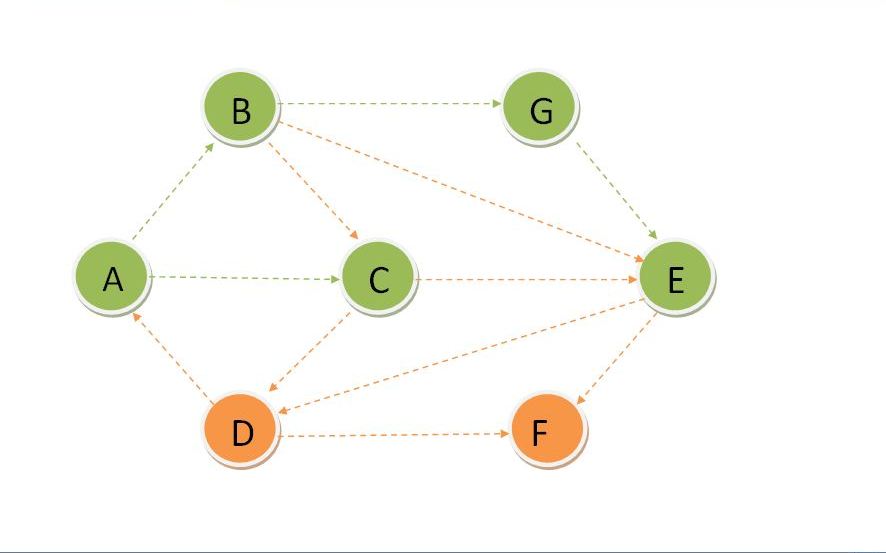
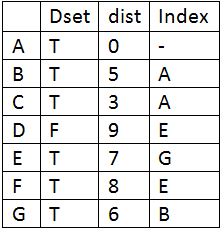
Update Dset for F and update distance of its adjacent vertices and find the vertex with minimum distance which is D.

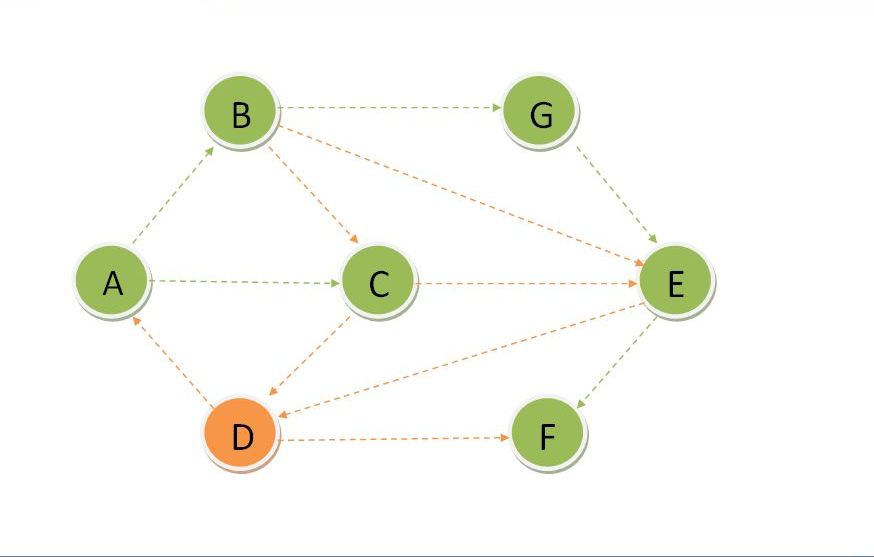
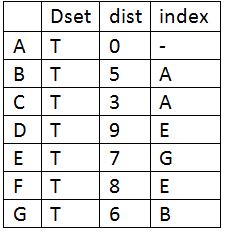
Update Dset for D.

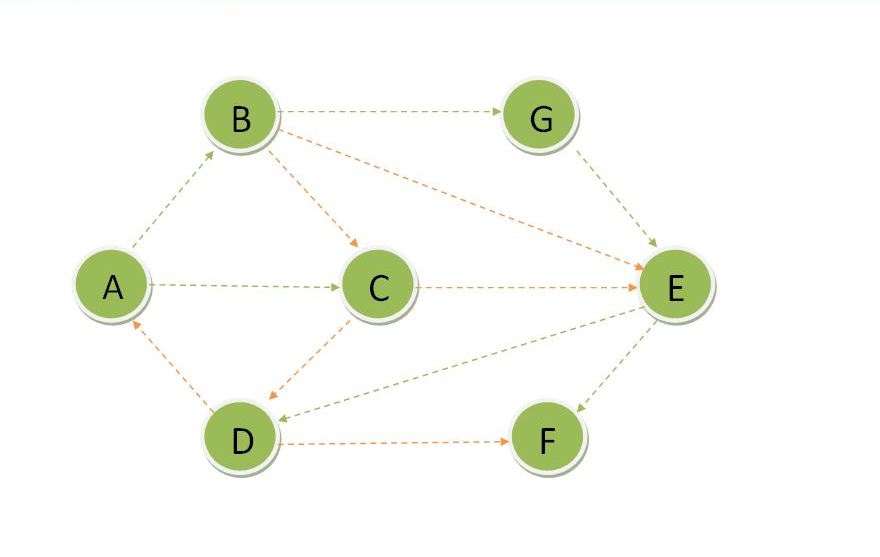
As all the vertices are part of Dset so we got the shortest path which contains all the vertices. So the graph for shortest path from vertex A is

C++ Program to Implement Dijkstra's Algorithm

#include <iostream>
#include <climits> // Used for INT_MAX
using namespace std;

// It is the total no of verteices in the graph
#define vertex 7

// A method to find the vertex with minimum distance
// which is not yet included in Dset
int minimumDist(int dist[], bool Dset[])
{
    // initialize min with the maximum possible value
    // as infinity does not exist
    int min = INT_MAX, index;
    for (int v = 0; v < vertex; v++) {
        if (Dset[v] == false && dist[v] <= min) {
            min = dist[v];
            index = v;
        }
    }
    return index;
}

// Method to implement shortest path algorithm
void dijkstra(int graph[vertex][vertex], int src)
{
    int dist[vertex];
    bool Dset[vertex];
    // Initialize distance of all the vertex
    // to INFINITY and Dset as false
    for (int i = 0; i < vertex; i++) {
        dist[i] = INT_MAX;
        Dset[i] = false;
    }
    // Initialize the distance of the source vertec to zero
    dist[src] = 0;
    for (int c = 0; c < vertex; c++) {

        // u is any vertex that is not yet included in
        // Dset and has minimum distance
        int u = minimumDist(dist, Dset);
        // If the vertex with minimum distance found
        // include it to Dset

        Dset[u] = true;
        // Update dist[v] if not in Dset and their is a path from src to v
        // through u that has distance minimum than current value of dist[v]
        for (int v = 0; v < vertex; v++) {
            if (!Dset[v] && graph[u][v] && dist[u] != INT_MAX && dist[u] + graph[u][v] < dist[v])
                dist[v] = dist[u] + graph[u][v];
        }
    }
    cout << "Vertex\t\tDistance from source" << endl;
    // will print the vertex with their distance
    // from the source to the console
    for (int i = 0; i < vertex; i++) {
        char c = 65 + i;
        cout << c << "\t\t" << dist[i] << endl;
    }
}

// Main program
int main()
{
    int graph[vertex][vertex] = { 
        { 0, 5, 3, 0, 0, 0, 0 }, 
        { 0, 0, 2, 0, 3, 0, 1 }, 
        { 0, 0, 0, 7, 7, 0, 0 }, 
        { 2, 0, 0, 0, 0, 6, 0 }, 
        { 0, 0, 0, 2, 0, 1, 0 }, 
        { 0, 0, 0, 0, 0, 0, 0 },
        { 0, 0, 0, 0, 1, 0, 0 } 
    };
    
    dijkstra(graph, 0);
    
    return 0;
}

Output

Vertex      Distance from source
A               0
B               5
C               3
D               9
E               7
F               8
G               6