Home » C++ programming language

Maximum Sum Helix path (using C++ program)

Learn: C++ program to find maxsum of double helix - How to find a path that produces the maximum sum of elements on your path you walked over?

Maximum Sum Helix path

Question

Given two finite, strictly increasing, integer sequences. Any common integer between the two sequences constitutes an intersection point; you have to find a path that produces the maximum sum of elements on your path you walked over.

You can 'walk' over these two sequences in the following way:

1. You may start at the beginning of any of the two sequences. Now start moving forward.
2. At each intersection point, you have the choice of either continuing with the same sequence you are currently on, or switching to the other sequence.

Example

Input:
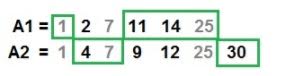
A1[] = 1 2 7 11 14 25 
A2[] = 1 4 7  9 12 25 30

Output : The largest possible sum = 92

Idea

We will maintain three variables path1, path2 and pathsum. At any instant, path1 is the maximum sum of data we walked over till now, being on sequence 1. path2 is the maximum amount of data we walked over till now, being on sequence 2. The final result is stored in variable pathsum by which is the maximum of path1 and path2.

As we proceed in processing the sequence we sum all elements of sequence 1 and sequence 2 in path1 and path2 respectively till we reach any intersecting point. After reaching any intersecting point we should add greater of path1 or path2 to pathsum and reset path1 = path2 = 0 and start processing sequences further. In the case we end up any sequence we should add all remaining elements of next sequence to its corresponding path and finally check for greater of both the paths and add the greater to pathsum.

C++ program to find maxsum of double helix

#include<bits/stdc++.h>
using namespace std;

// function for calculation of largest sum
int maxSumDHelix(int A1[], int A2[], int n1, int n2)
{
  int i, j = 0, path1 = 0, path2 = 0, pathsum = 0;

    // n1, n2 are length of both sequences
    for(i=0; i<n2; i++)
    {
       // add elements to path2
       path2 += A2[i];

       // add elements to pat1
       while(j<n1 && A1[j] < A2[i])
       {
           path1 += A1[j];
           j++;
       }

       // at intersection point update
       // path1 path2 and pathsum
       if(j<n1 && A1[j]==A2[i])
       {
            path1 += A1[j];
            pathsum += max(path1, path2);

            //reset
            path1 = 0;
            path2 = 0;
            j++;
       }
    }

    // if n1 &amp;gt; n2
    while(j<n1)
    {
        path1 += A1[j];
        j++;
    }
    // final result
    pathsum += max(path1, path2);
    return pathsum;
}


// driver program
int main()
{
    int n1,n2;
    cout<<"Enter size of 1st array :";
    cin>>n1;
    int A1[n1];
    cout<<"\nEnter elements of 1st array:\n";
    for(int i=0;i<n1;i++)
        cin>>A1[i];
    cout<<"Enter size of 2nd array:";
    cin>>n2;
    int A2[n2];
    cout<<"\nEnter elements of 2nd array:\n";
    for(int i=0;i<n2;i++)
        cin>>A2[i];
    cout << "The largest possible sum = " << maxSumDHelix(A1, A2, n1, n2);
    return 0;
}

Output

Enter size of 1st array :6

Enter elements of 1st array:
1 2 7 11 14 25
Enter size of 2nd array:7 

Enter elements of 2nd array:
1 4 7 9 12 25 30
The largest possible sum = 92