Home » Computer Graphics

Defining a Circle in Computer Graphics

Computer Graphics | Defining a Circle: This tutorial is on the concept of defining a circle in computer graphics. Here, we will learn how we define a circle in mathematics, and then will see how we can implement the same using computer graphics programs? By Monika Sharma Last updated : April 05, 2024

After studying the implementation of lines in computer graphics, we will now be dealing with how to draw different polygons and shapes using programs, and we will be first starting with the circle.

What is a circle?

A circle is defined as a set of points that all are the same distance from a common point. The common point is known as the center and the distance from the center of the circle to any point on its circumference is called the radius.

It is an eight-way symmetric figure which can be divided into four quadrants and each quadrant has two octants. This symmetry helps in drawing a circle on a computer by knowing only one point of any octant.

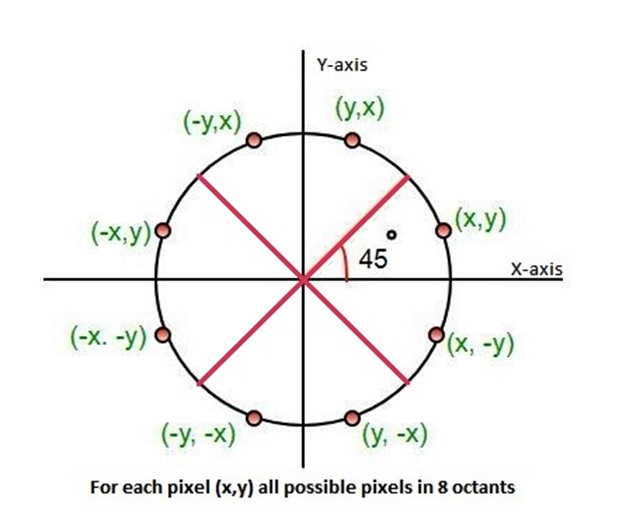
How to define a circle in computer graphics?

There are two methods to define a circle in computer graphics, namely:

1. Direct or Polynomial method and
2. Polar coordinates method

Let us have a look at both these methods and learn about them in brief.

1. Direct or Polynomial Method

In this method, a circle is defined with the help of a polynomial equation i.e.

    (x - xc)2  + (y - yc)2  =  r2

Where, (x_c, y_c) are coordinates of circle and r is radius of circle.

For each value of x, value of y can be calculated using,

    y = yc ± √r2 – (x - xc)2

The initial points will be: x = x_c – r, and y = y_c

This is a very ineffective method because for each point value of x_c, x and r are squared and then subtracted and then the square root is calculated, which leads to high time complexity.

2. Polar coordinates Method

In this method, the coordinates are converted into polar coordinates. The coordinates are thus given by:

    x = r cosθ              ...(1)
    y = r sinθ              ...(2)
    r = radius
    Where, θ = current angle

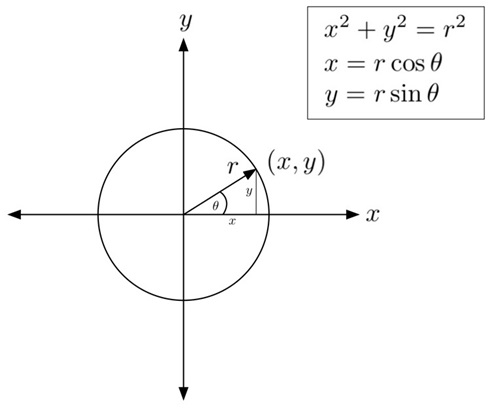
For the first octant i.e. from θ = 0⁰ to θ = 45⁰,

The values of x and y are calculated using equations (1) and (2).

Simultaneously, all the eight points for the rest of the octants can be calculated using the eight-way symmetry property of the circle.

Then, the plotting of the circle is done.

We will study this plotting through various algorithms in the upcoming sections.