Home » Computer Graphics

Scaling in Computer Graphics

Computer Graphics | Scaling: In this tutorial, we are going to learn about Scaling which is a type of Transformation in computer graphics, type of Transformation in brief, etc. By Monika Sharma Last updated : April 05, 2024

Scaling

Scaling is a process of modifying or we can say changing the size of objects. It is a type of transformation through which we can zoom in or zoom out any particular object or shape.

We can say that it is the process of expanding or compressing the dimension of an object. There are two factors used in scaling transformation i.e. Sx and Sy, where Tx is a scale factor for the co-ordinates, and Ty is the scale factor for the Y coordinates. Whereas, scaling changes the size of an object and involves two scale factors, Sx and Sy for the x- and y- coordinates respectively.

Uniform Scaling

If Sx and Sy are equal it is also called Uniform Scaling, If not equal then it is called Differential Scaling.

Points to remember:

Scales are about the origin.

We can write them as

    X' = sx • Xold
    Y' = sy • Yold

In matrix form it is written as follows:

    P' = S • P 

Suppose if scaling factors with values less than one will move the object closer to co-ordinate origin, while a value higher than one will move co-ordinate position farther from the origin.

Now let's understand with the help of a figure.

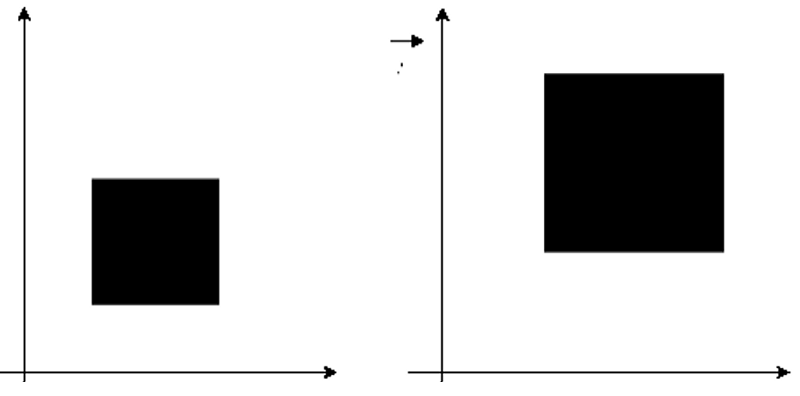
More accurately we can say that scaling can be used to increase or decrease which is reduce the size of the object. Scaling subjects to the co-ordinate points of the original object are to be changed. Here scaling factor determines whether the size of the object is to be increase or decrease.

One thing which we should keep in mind and which is going to make scaling easier for us to remember:

• If the scaling factor > 1, then the object size is increased, i.e., we zoom in.
• If the scaling factor < 1, then the object size is decreased, i.e. we zoom out.

Scaling Example

Now let's see the same with the help of an example:

Problem Statement: Given a square object with co-ordinate points A (0, 3), B (3, 3), C (3, 0), D (0, 0). Apply the scaling parameter 2 towards X axis and 3 towards Y axis and obtain the new co-ordinates of the object.

Solution:

Given,

• Old corner coordinates of the square = A (0, 3), B (3, 3), C (3, 0), D (0, 0)
• Scaling factor along X axis = 2
• Scaling factor along Y axis = 3

For the Coordinate A (0, 3):

Let the new coordinates of corner A after scaling = (X_new, Y_new).

When we apply the scaling equation, we get,

X_new = X_old x S_x = 0  x 2 = 0
Y_new = Y_old x S_y = 3 x 3 = 9

Thus, the new coordinates of corner A after scaling = (0, 9).

For the Coordinate B (3, 3):

Let the new coordinates of corner B after scaling = (X_new, Y_new).

When we apply the scaling equation, we get-

X_new = X_old x S_x = 3  x 2 = 6
Y_new = Y_old x S_y = 3 x 3 = 9

Thus, the new coordinates of corner B after scaling = (6, 9).

For the Coordinate C (3, 0):

Let the new coordinates of corner C after scaling = (X_new, Y_new).

When we apply the scaling equation, we get-

X_new = X_old x S_x = 3 x 2 = 6
Y_new = Y_old x S_y = 0 x 3 = 0

Thus, the new coordinates of corner C after scaling = (6, 0).

 For the Coordinate D (0, 0):

Let the new coordinates of corner D after scaling = (X_new, Y_new).

When we apply the scaling equation, we get-

X_new = X_old x S_x = 0  x 2 = 0
Y_new = Y_old x S_y = 0 x 3 = 0

Thus, the new coordinates of corner D after scaling = (0, 0).

Thus, New coordinates of the square after Aaplying the scaling parameter 2 towards X axis and 3 towards Y axis are = A (0, 9), B (6, 9), C (6, 0), D (0, 0).