Home » Computer Graphics

Translations in Computer Graphics

Computer Graphics | Translations: In this tutorial, we are going to learn about Translation which is a type of Transformation in computer graphics, type of Transformation in brief, etc. By Monika Sharma, on April 30, 2020

Translations

Translation techniques mean to modify the current shape or object in a particular manner. Changing of an object after creation, in terms of position or even size is known as translation. Here, we will be studying about how 2D translation is performed in computer graphics.

2D Translation

The translation is the movement in a straight line of an object from one position to another.

The movement of objects without deforming the shape of the object is Translation. Here the object is shifted from one position to another position and from one co-ordinate location to another.

The translating polygon i.e. all vertex of the polygon is converted to a new position. Similarly, curved objects are translated. To change the position of the circle or ellipse its center coordinates are transformed, then the object is drawn using the new co-ordinates.

Translation of Point

To translate a point from coordinate position (x, y) to another (x, y), we add algebraically the translation distances Tx & Ty to the original co-ordinates.

Translation Equation

x1 = x + Tx
y1 = y + Ty 	
(The translation pair (Tx, Ty) is called as shift vector)

Example:

In the following image you can see that after applying translation, point C gets shifted to C'.

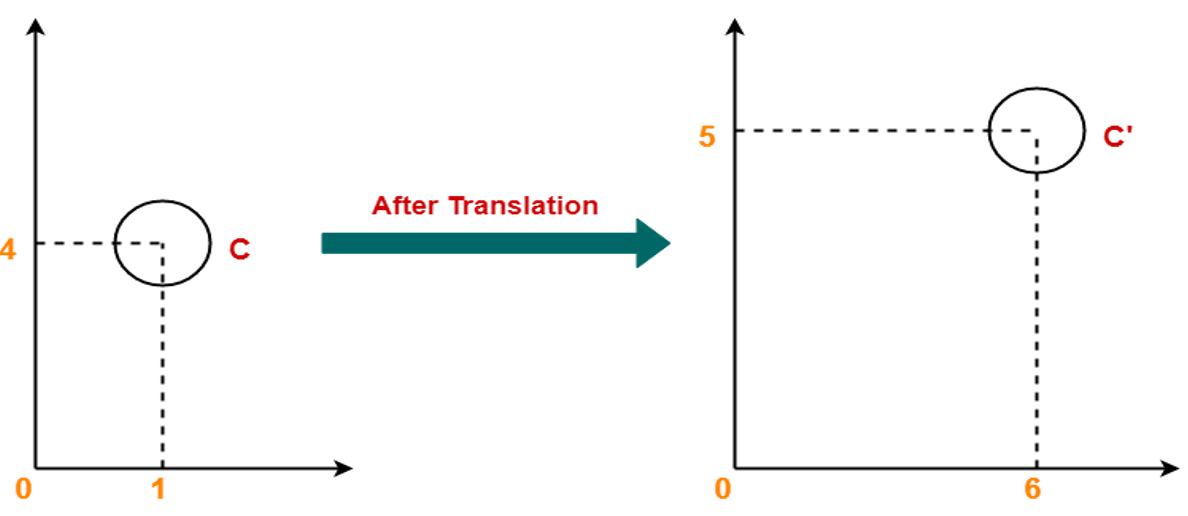
Example

Given a square with coordinate points A (0, 3), B (3, 3), C (3, 0), D (0, 0). Apply the translation with distance 1 towards X axis and 1 towards Y axis. We have to find the new co-ordinates of the square.

Solution:  Given-

Old co-ordinates of the square = A (0, 3), B (3, 3), C (3, 0), D (0, 0)

Translation vector = (Tx, Ty) = (1, 1)

For Coordinates A (0, 3)

 Let the new coordinates of corner A = (X_new, Y_new).

Applying the translation equations, we have-

• X_new= X_old + T_x = 0 + 1 = 1
• Y_new= Y_old + T_y = 3 + 1 = 4

Thus, New coordinates of corner A = (1, 4).

For Coordinates B (3, 3)

Let the new coordinates of corner B = (X_new, Y_new).

Applying the translation equations, we have-

• X_new= X_old + T_x = 3 + 1 = 4
• Y_new= Y_old + T_y = 3 + 1 = 4

Thus, New coordinates of corner B = (4, 4).

For Coordinates C (3, 0)

Let the new coordinates of corner C = (X_new, Y_new).

Applying the translation equations, we have-

• X_new= X_old + T_x = 3 + 1 = 4
• Y_new= Y_old + T_y = 0 + 1 = 1

Thus, New coordinates of corner C = (4, 1).

For Coordinates D (0, 0)

Let the new coordinates of corner D = (X_new, Y_new).

Applying the translation equations, we have-

• X_new= X_old + T_x = 0 + 1 = 1
• Y_new= Y_old + T_y = 0 + 1 = 1

Thus, New coordinates of corner D = (1, 1).