Home » Computer Graphics

Rotation in Computer Graphics

Computer Graphics | Rotation: In this tutorial, we are going to learn about the Rotation which is a type of Transformation in computer graphics, type of Transformation in brief, etc. By Monika Sharma Last updated : April 05, 2024

Rotation

Rotation is a type of transformation that is very often used in computer graphics and image processing. Rotation is a process of rotating an object concerning an angle in a two-dimensional plane.

It is a process of changing the angle of the object which can be clockwise or anticlockwise, while we have to specify the angle of rotation and rotation point. A rotation point is also called a pivot point.

Types of Rotations

There are two types of rotations according to the direction of the movement of the object. These are:

• Anti-clockwise rotation
• Clockwise rotation

The positive value of the rotation angle rotates an object in an anti-clockwise direction while the negative value of the rotation angle rotates an object in a clockwise direction. When we rotate any object, then every point of that object is rotated by the same angle. For example, a straight line is rotated by the endpoints with the same angle and the line is re-drawn between the new endpoints. Also, the polygon is rotated by shifting every vertex with the help of the same rotational angle. Same for circle also, it can be obtained by center position by the specified angle.

Let's now consider a point object O which has to be rotated from one angle to another.

• Initial co-ordinates of the object O = (X_old, Y_old)
• Initial angle of the object O with respect to origin = Φ
• Rotation angle = θ
• New co-ordinates of the object O after rotation = (X_new, Y_new)

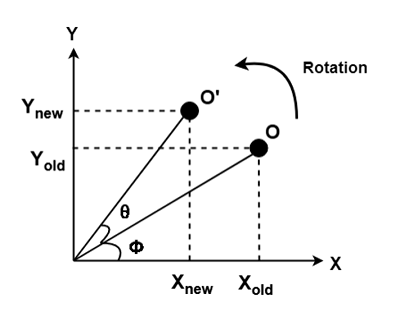
In order to rotate an object, we need to rotate each vertex of the figure individually. More clearly let us assume a point P, on rotating a point P(x, y) by an angle A about the origin we get a point P' (x', y'). The calculation of values of x' and y' are as follows,

We know that,

    x   = r cosB, y = r sinB
    x'  = r cos ( A + B)
        = r ( cosA cosB – sinA sinB ) 
        = r cosB cosA – r sinB sinA 
        = x cosA – y sinA
    y'  = r sin ( A + B ) 
        = r ( sinA cosB + cosA sinB )  
        = r cosB sinA + r sinB cosA 
        = x sinA + y cosA

It's representation in matrix form will be as follows,

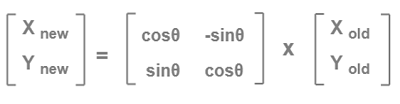
Rotation Example

Now let's understand this by using an example,

Problem Statement: Given a triangle with corner coordinates (0, 0), (1, 0) and (1, 1). Rotate the triangle by 90 degrees anticlockwise direction and find out the new coordinates.

Solution:
We always rotate a polygon by rotating each of its vertexes with the same rotation angle.

Given,

• Old corner coordinates of the triangle = A (0, 0), B (1, 0), C (1, 1)
• Rotation angle = θ = 90º

For the Co-ordinate A (0, 0)

Let the new coordinates of corner A after rotation = (X_new, Y_new).

When we apply the rotation equation, we get-

X_new = X_old x cosθ – Y_old x sinθ

         = 0 x cos90º – 0 x sin90º

         = 0 + 0

         = 0

 

Y_new = X_old x sinθ + Y_old x cosθ

        = 0 x sin90º + 0 x cos90º 

       = 0 + 0

       = 0

Thus, the new co-ordinates of corner A we get after rotation is = (0, 0).

For the Coordinate B (1, 0)

Let the new coordinates of corner B after rotation = (X_new, Y_new).

X_new = X_old x cosθ – Y_old x sinθ

        = 1 x cos90º – 0 x sin90º

        = 0 – 0

        = 0

Y_new = X_old x sinθ + Y_old x cosθ

        = 1 x sin90º + 0 x cos90º

       = 1 + 0

       = 1

Thus, the new co-ordinates of corner B that we get after rotation are = (0, 1).

For the Coordinate C (1, 1)

Let the new coordinates of corner C after rotation = (X_new, Y_new).

X_new = X_old x cosθ – Y_old x sinθ

         = 1 x cos90º – 1 x sin90º

         = 0 – 1

         = -1

Y_new = X_old x sinθ + Y_old x cosθ

        = 1 x sin90º + 1 x cos90º

        = 1 + 0

        = 1

Thus, the new co-ordinates of corner C we get after rotation is = (-1, 1).

Thus, the new co-ordinates of the triangle after rotation are = A (0, 0), B (0, 1), C (-1, 1).