Home » Cryptography

Birthday Attack in Cryptography

Cryptography | Birthday Attack: In this tutorial, we will briefly study the basis of birthday attack and examples aim to capture. We will cover types of messages in Birthday Attack. By Monika Sharma Last updated : May 25, 2023

What is Birthday Attack in Cryptography?

That is, this attack can be used to abuse communication between two or more parties in cryptography. Thus, the attack is based on the higher likelihood of collisions found between random attack attempts and a fixed degree of permutations (pigeonhole) in cryptography. Thus, with a birthday attack, it is possible to find a collision of a hash function in 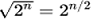, with 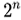being the classical preimage resistance security in this. Hence, there is a general as though disputed result that quantum computers can perform birthday attacks, thus breaking collision resistance, 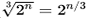in like this formula.

Birthday Problem

That is a set of randomly chosen people some pairs of them will have the same birthday in the year the cryptography.

Thus, the pigeonhole principle in the probability reaches 100% when the number of people reaches 367 since there are 366 possible birthdays, including February 29 this year in cryptography.

Whenever 99.9% probability is reached with just 70 people and 50% probability with 23 people overall. Thus, these conclusions include the assumption that each day of the year (except February 29) is equally probable for a birthday every year.

Which uses this probabilistic model to reduce the complexity of finding a collision for a hash function cryptography in cryptography in cryptoanalysis.

Mathematical base of Birthday Problem

Thus, the main problem is to compute the approximate probability that in a group of n people, at least two have the same birthday in the same year.

Hence, the aim is to compute P(A), the probability that at least two people in the room have the same birthday in the same year.

Wherever, it is easier to calculate P(A'), the probability that no two people in the room have the same birthday in the same year. Thus, because A and A' are the only two possibilities and are also mutually exclusive as follow,

P(A) = 1 − P(A').

Thus, when events are independent of each other the probability of all of the events occurring is equal to a product of the probabilities of each of the events occurring in the algorithm. Hence, if P(A') can be described as 23 independent events, P(A') could be calculated as follow,

P(1) × P(2) × P(3) × ... × P(23).

Then, the 23 independent events correspond to the 23 people and can be defined in the order to manage. Thus, each event can be defined as the corresponding person not sharing his or her birthday with any of the previously analyzed people by this birthday attack.

Thus, for Event 1, there are no previously analyzed people in the birthday attack. Wherever, the probability as P(1), that Person 1 does not share his/her birthday with previously analyzed people is 1, or 100% to get the perfect birthdate.

When ignoring leap years for this analysis the probability of person 1 can also be written as 365/365 in this, for reasons that will become clear below as follow.

And, for Event 2 the only previously analyzed people are Person 1 in this way. Then, assuming that birthdays are equally likely to happen on each of the 365 days of the year, the probability as P(2), that Person 2 has a different birthday than Person 1 is 364/365 in that way. Then, this is because if Person 2 was born on any of the other 364 days of the year, Persons 1 and 2 will not share the same birthday in the same year.

Whenever, if Person 3 is born on any of the 363 days of the year other than the birthdays of Persons 1 and 2, Person 3 will not share their birthday in the same year. Thus, this makes the probability as P(3) = 363/365.

Thus, P(A') is equal to the product of these individual probabilities as follow as given:

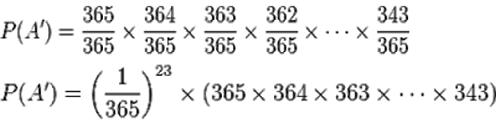
Finally, P(A') = 0.492703.

Hence, now as P(A)=1-P(A') then

P(A)= 1- 0.492703= 0.507297 or 50.7%

Thus, so the possibility of 2 people in a group of 23 people has the same birthday is 50.7% in the same year.