Home »
Cryptography
Message-Digest Algorithm 5 (MD5) in Cryptography
Cryptography | Message-Digest Algorithm 5 (MD5): In this tutorial, we will briefly study the basic MD5 notations, functionality and examples aim to capture. We will cover the types of messages in MD5.
By Monika Sharma Last updated : May 24, 2023
What is Message-Digest Algorithm 5 (MD5) in Cryptography?
In cryptography, MD5 (Message-Digest algorithm 5) is a mainly used cryptographic hash function with a 128-bit hash value. As we use in an Internet standard (RFC 1321), MD5 has been employed or developed in a more variety of security applications and is also mainly used to check the integrity of files or the product. An MD5 hash is expressed as a 32 digit hexadecimal number in it.
MD5 is a strengthened or latest version of MD4. Similarly, like MD4, the MD5 hash was invented by "Professor Ronald Rivest" of MIT University. Also, MD5 was used as the model for SHA-1, since they sharing many common features between them. MD5 and SHA-1 are the two most mainly used hash algorithms nowadays, but the use of MD5 will certainly decline over time since it is now considered broken.
The Algorithm
The MD5 hash technique is described in "RFC 1321" along with a C implementation. MD5 is similar to the MD4 hash. The padding is identical.
MD5 works on 32-bit words. Let the required message to be implemented is "M".
The message "M" is padded so that its length in bits is similar to 448 modulo 512, that is, the padded message is less than 64 bits of multiple of 512.
Firstly, the padding consists of a single 1 bit in the first column, followed by enough zeros to pad the message to the required length till the 512 bit. Padding is always used, even if the original length of M happens to equal 448 mod 512. As a result, there is at least one bit of padding, and at most 512 bits of padding. Then the length in bits of the message uses before padding is appended as a 64-bit block.
The padded message is a multiple of 512 bits and, it is also a multiple of 32 bits.
Let M be the required message and N is the number of 32-bit words used in the padded message. Due to the actual padding, N is a multiple of 16 bit.
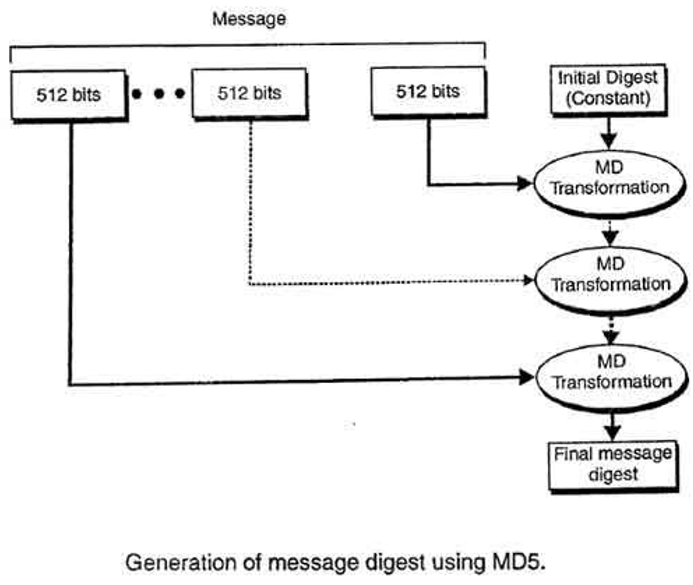
There is a four-word buffer (A, B, C, D) is used to generate the message digest. Here each of A, B, C, D is a 32-bit buffer for a use. These buffer words are initialized to the following values in hexadecimal as follow,
word A: 01 23 45 67
word B: 89 ab cd ef
word C: fe dc ba 98
word D: 76 54 32 10
We first define the four auxiliary functions which use in the buffer that each takes as input three 32-bit words and produces as output one 32-bit word.
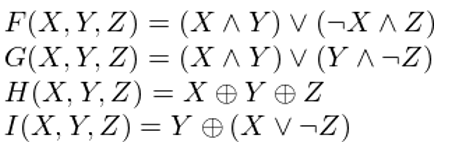
here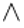 
it is logical "and", 
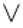it is logical "or" and 
is logical "xor".
The uses of the four buffers (A, B, C, and D) are now combined with the words of the input using the four auxiliary functions (F, G, H and I). Here, there are four rounds, each involves 16 basic operations to perform. One operation is shown in the figure below,
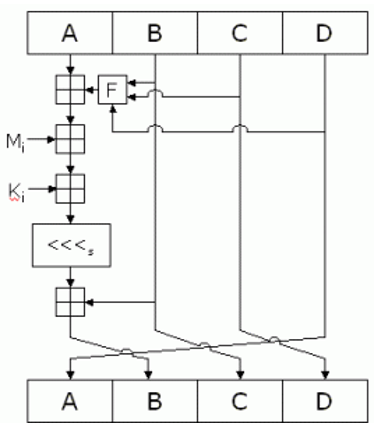
The figure shows how the auxiliary function "F" is used to the four buffers (A, B, C, and D), using the message word "M(i)" and constant "K(i)." The item "<<<n" denotes a binary left shift by n bits.
The output
After we perform all rounds, the buffers A, B, C, and D contain the MD5 digest of the original input.
Mainly, MD5 has five steps with four rounds of computations that compute the hash of the input value and gave the buffer output.
References