Home » Cryptography

International Data Encryption Algorithm (IDEA) in Cryptography

In this tutorial, we will learn about the international data encryption algorithm (IDEA), its block diagram, its steps of encryption and decryption, and security. By Monika Sharma Last updated : May 25, 2023

What is International Data Encryption Algorithm (IDEA) in Cryptography?

International Data Encryption Algorithm (IDEA) is a type of cryptography as a block cipher algorithm designed by "Xuejia Lai" and "James L.Massey" of ETH-Zürich and was first published in the 1991 year. Then, the original algorithm went through a few modifications and finally named as International Data Encryption Algorithm (IDEA) as follows. The mentioned algorithm works on 64-bit plain text and cipher text block at one time in the algorithm. Then, For encryption, the 64-bit plain text is divided into four 16 bits sub-blocks of the algorithm. In our discussion, we denote these four blocks as P1 (16 bits), P2 (16 bits), P3 (16 bits) and P4 (16 bits) as the divide of 4 blocks. Here, each of these blocks goes through 8 ROUNDS and one OUTPUT TRANSFORMATION phase at the end of the operation. In each of these eight rounds, some as arithmetic and logical operations are performed by this algorithm. Therefore, the eight ROUNDS are the same sequences of operations are repeated after every round in the cryptography.International Data Encryption Algorithm (IDEA) is a type of cryptography as a block cipher algorithm designed by "Xuejia Lai" and "James L.Massey" of ETH-Zürich and was first published in the 1991 year. Then, the original algorithm went through a few modifications and finally named as International Data Encryption Algorithm (IDEA) as follows. The mentioned algorithm works on 64-bit plain text and cipher text block at one time in the algorithm. Then, For encryption, the 64-bit plain text is divided into four 16 bits sub-blocks of the algorithm. In our discussion, we denote these four blocks as P1 (16 bits), P2 (16 bits), P3 (16 bits) and P4 (16 bits) as the divide of 4 blocks. Here, each of these blocks goes through 8 ROUNDS and one OUTPUT TRANSFORMATION phase at the end of the operation. In each of these eight rounds, some as arithmetic and logical operations are performed by this algorithm. Therefore, the eight ROUNDS are the same sequences of operations are repeated after every round in the cryptography.

At the last phase, i.e., the OUTPUT TRANSFORMATION phase, we perform only arithmetic operations with 4 keys in the cryptography.  International Data Encryption Algorithm (IDEA) is a type of cryptography as a block cipher algorithm designed by "Xuejia Lai" and "James L.Massey" of ETH-Zürich and was first published in the 1991 year. Then, the original algorithm went through a few modifications and finally named as International Data Encryption Algorithm (IDEA) as follows. The mentioned algorithm works on 64-bit plain text and cipher text block at one time in the algorithm. Then, For encryption, the 64-bit plain text is divided into four 16 bits sub-blocks of the algorithm. In our discussion, we denote these four blocks as P1 (16 bits), P2 (16 bits), P3 (16 bits) and P4 (16 bits) as the divide of 4 blocks. Here, each of these blocks goes through 8 ROUNDS and one OUTPUT TRANSFORMATION phase at the end of the operation. In each of these eight rounds, some as arithmetic and logical operations are performed by this algorithm. Therefore, the eight ROUNDS are the same sequences of operations are repeated after every round in the cryptography. At the last phase, i.e., the OUTPUT TRANSFORMATION phase, we perform only arithmetic operations with 4 keys in the cryptography.

It is an IDEA, unlike the other block cipher algorithms is studied by the Swiss firm of Ascom. However, be unique in permit with permission with free noncommercial use of their algorithm which the result that IDEA is best known as the block cipher algorithm used within the popular encryption for the message character.The algorithm is suggested in its own right. It has some steps which make it appear that it might be a non-invertible hash function instead of a block cipher in the cryptography. Also, it is told in that it entirely ignores the use of any S-boxes or given lookup table in the cryptography.

Here, IDEA uses 52 subkeys and every 16 bits long of character. Here, two are used during each round in the IDEA proper and four are used before every round and after the last round. It has eight rounds and at last output round which includes 4 keys.The original text or plaintext block in IDEA is divided into four blocks and each 16 bits long. Mainly, three operations are used in IDEA to combine two 16 bit values to produce a 16-bit result as ciphertext as addition, XOR, and multiplication. Here,  Addition is normal addition with carries the modulo 65,536. Multiplication, as used in IDEA, requires some need for explanation.

Now, Multiplication by zero always produces zero and is not invertible in the message. Multiplication modulo n is also not invertible whenever it is by a number that is not relatively prime to n like this. The main single way multiplication is used in IDEA, it must be always invertible in the message form in the cryptography.

Block Diagram of IDEA

The block diagram of International Data Encryption Algorithm (IDEA) is:

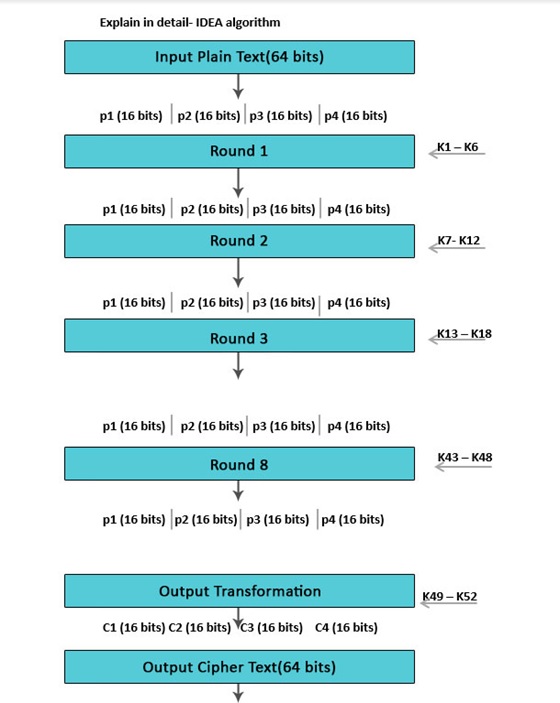
The plaintext of 64-bit input block-divided into 4 part (16 bits each) Declare p1 to p4:

• Therefore, from plaintext p1 to p4 will be the inputs for the initial round of the algorithm in this.
• Here, are 8 such rounds.
• Then, the key is made up of 128 bits.
• In every round, 6 sub-keys will be produced by key generation.
• Each one of the sub-keys includes 16 bits of character.
• All these sub-keys will be put on the 4 input blocks p1 to p4 in the operation.
• There will be last actions include Output Transformation which usually benefits simply 4 sub-Keys at the last key generation.
• The last output created is 4 blocks of ciphertext C1 to C4 as each one of 16 bits and combine them to make a ciphertext.
• They are mixed to create the last 64-bit ciphertext block by this operation.

International Data Encryption Algorithm (IDEA) Encryption

Output Transformation

• It can be done a one-time procedure.
• They require places by the end of the 8th round in the operation.
• Here, the input towards the Output transformation is, a 64-bit value divided into 4 sub-blocks (state R1 to R4 every among 16 bits) from the message.
• The cryptography bit of four 16 bits Sub-keys (K1 to K4) is used here.
• Now, the process of the outcome transformation can be as follows until now.

International Data Encryption Algorithm (IDEA) Decryption

The Decryption implements like encryption, but the order of the round keys is generated, and the subkeys for the odd rounds are inversed into this. Therefore, the values of subkeys K1-K4 are replaced by the inverse of K49-K52 for the respective group operation in the cryptography, K5, and K6 of each group should be replaced by K47 and K48 for decryption in this operation in the cryptography.

International Data Encryption Algorithm (IDEA) Security

The implemented analyzed IDEA to measure its strength against differential cryptoanalysis and concluded that it is immune under certain assumptions in this. No successful linear or algebraic weaknesses have been reported for this view. In fact of 2007, the best attack applied to all keys could break IDEA reduced to 6 rounds as the full IDEA cipher uses 8.5 rounds as having output transformation in last having 4 keys. Required, that a "break" is an attack that requires less than 2128 operations into this algorithm; the 6-round attack requires 264 known plaintexts or original text and 2126.8 operations for the algorithm in the cryptography.The implemented analyzed IDEA to measure its strength against differential cryptoanalysis and concluded that it is immune under certain assumptions in this. No successful linear or algebraic weaknesses have been reported for this view. In fact of 2007, the best attack applied to all keys could break IDEA reduced to 6 rounds as the full IDEA cipher uses 8.5 rounds as having output transformation in last having 4 keys. Required, that a "break" is an attack that requires less than 2128 operations into this algorithm; the 6-round attack requires 264 known plaintexts or original text and 2126.8 operations for the algorithm in the cryptography.

The Bruce Schneier thought highly of IDEA in 1996, writing as follows: "According to my opinion, it is the best and most secure block algorithm available to the public at this time for the algorithm." Wherever, by 1999 he was no longer recommending IDEA due to the availability of faster algorithms, some progress in its cryptanalysis, and the issue of patents in the cryptography cryptoanalysis.Since in 2011  the full 8.5-round of IDEA was break using a meet-in-the-middle attack by this algorithm. In fact, in 2012, full 8.5-round IDEA was broken using a narrow-bicliques attack, with a reduction of cryptographic strength of about 2 bits of the character, similar to the effect of the previous bicliques attack on AES; however, this attack does not threaten the security of IDEA in practice in the algorithm of cryptography.

It will very secure and safe to implement or encrypt or decrypt by this algorithm IDEA.

Image source: https://www.educba.com/idea-algorithm/