Home » Operating System

Preemptive Priority Scheduling Algorithm

In this tutorial, we will learn about the preemptive priority scheduling algorithm in an operating system with the help of an example. By Monika Sharma Last updated : May 07, 2023

What is a preemptive priority scheduling algorithm?

In the priority scheduling, the processes are scheduled on the basis of their priority, and not on the basis of their burst time. If the preemptive mode of this scheduling is being followed, then a process with a higher priority than the currently executing process can replace the executing process. This can be well explained with the help of the following example.

Preemptive Priority Scheduling Algorithm Example

Suppose, we have four processes: P1, P2, P3 and P4, and they enter the CPU in the following manner:

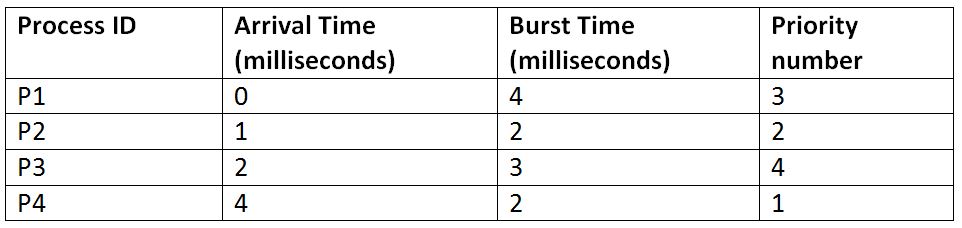
As per the preemptive priority scheduling, the processes will be executed as follows:

Gant Chart

Explanation

• There is only P1 available at time 0, so it will be executed first irrespective of the priority until some other process with a higher priority is encountered by the OS.
• At the beginning of the 1^st-time unit, we have P2 which has a higher priority than P1, so it replaces P1.
• At 2^nd time unit, we have the process P3, but its priority is less than the executing process P2, so P2 keeps executing without any replacement.
• At 3^rd time unit, our P2 has been completed and till now we have processes P1 and P3 left. So, P1 which has a higher priority than P3 is executed.
• At 4^th time unit, we have process P4 which has the highest priority of them all. So, it replaces P1.
• Since now we have no more processes left to arrive, the processes will now run according to their priorities and will complete their execution.

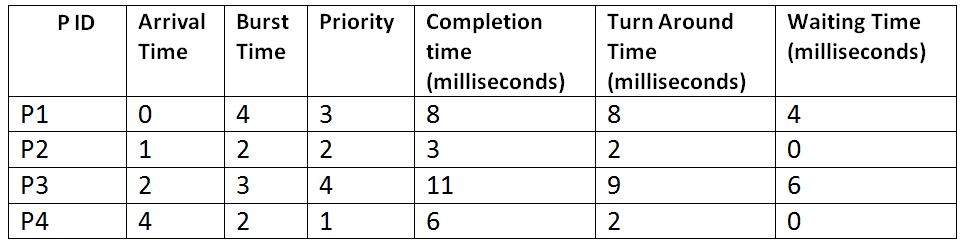
Total Turn-Around Time = 8 + 2 + 9 + 2
            = 21 milliseconds
Average Turn-Around Time= Total Turn-Around Time / Total No. of Processes
            = 21 / 4
            = 5.25 milliseconds

Total Waiting Time = 4 + 0 + 6 + 0
            = 10 milliseconds
Average Waiting Time = Total Waiting Time / Total No. of Processes
            = 10 / 4
            = 2.5 milliseconds

---