Home » Algorithms

Bubble Sort Algorithm: What It is, Flow Chart, Time Complexity, and Implementation

Bubble Sort Algorithm: In this tutorial, we will learn about bubble sort, its algorithm, flow chart, and its implementation using C, C++, and Python. By Raunak Goswami Last updated : August 12, 2023

We are going to look at the algorithm of one of the simplest and the easiest sorting technique. since algorithm are language independent so you can use this algorithm to write your code in any language that you prefer.

Bubble Sort Algorithm

Bubble sort is the simplest sorting algorithm and is useful for small amounts of data, Bubble sort implementation is based on swapping the adjacent elements repeatedly if they are not sorted. Bubble sort's time complexity in both of the cases (average and worst-case) is quite high. For large amounts of data, the use of Bubble sort is not recommended.

The basic logic behind this algorithm is that the computer selects the first element and performs swapping by the adjacent element if required based on the kind of sorting i.e. ascending and descending till it reaches the last element this is known as a pass. The computer performs multiple such passes till all the elements are sorted or no more swapping is possible.

Bubble Sort Algorithm Pseudo Code

Consider the below-given pseudo code for implementing a bubble sort:

Bubble Sort(a[],n)
For i=0 to n-1
Swap=false
For j=i+1 to n
    if a[j-1] >a[j]
        Swap(a[j-1],a[j])
        Swap=true
    Break if not swapped

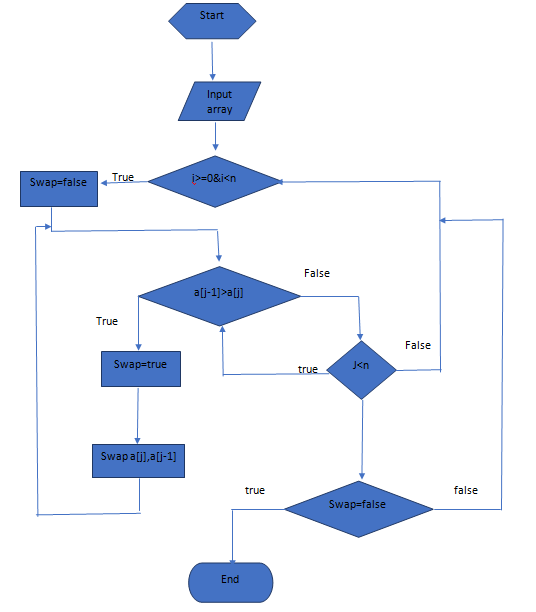
Bubble Sort Algorithm Flow chart

To help you understand better you can look at the flowchart for the bubble sort given below:

Bubble Sort Using C

The below is the implementation of bubble sort using C program:

#include <stdio.h>

void swap(int* x, int* y)
{
    int temp = *x;
    *x = *y;
    *y = temp;
}

void bubble_sort(int arr[], int n)
{
    int i, j;
    for (i = 0; i < n - 1; i++)
        for (j = 0; j < n - i - 1; j++)
            if (arr[j] > arr[j + 1])
                swap(&arr[j], &arr[j + 1]);
}

int main()
{
    int arr[] = { 12, 46, 34, 82, 10, 9, 28 };
    int n = sizeof(arr) / sizeof(arr[0]);

    printf("\nInput Array: \n");
    for (int i = 0; i < n; i++)
        printf("%d ", arr[i]);

    bubble_sort(arr, n);
    printf("\nSorted Array: \n");
    for (int i = 0; i < n; i++)
        printf("%d ", arr[i]);

    return 0;
}

The output of the above program will be:

Input Array:
12 46 34 82 10 9 28
Sorted Array:
9 10 12 28 34 46 82

Bubble Sort Using C++

The below is the implementation of bubble sort using C++ program:

#include <iostream>
using namespace std;

int main()
{
    int a[5];
    int temp;
    for (int i = 0; i < 5; i++) {
        cin >> a[i];
    }

    for (int j = 0; j < 4; j++) {
        for (int k = j + 1; k < 5; k++)
            if (a[j] > a[k]) {
                temp = a[k];
                a[k] = a[j];
                a[j] = temp;
            }
    }

    cout << "the elements after sorting" << endl;
    for (int i = 0; i < 5; i++)
        cout << a[i] << endl;

    return 0;
}

The output of the above program will be:

1
2
3
6
4
the elements after sorting
1
2
3
4
6

Bubble Sort Using Python

The below is the implementation of bubble sort using Python program:

import sys

def bubble_sort(arr):
    # This function will sort the array in non-decreasing order. 
    n = len(arr)
    #Traverse through all the array elements
    for i in range(n):
        # The inner loop will run for n-i-1 times as the
        # last i elements are already in place.
        for j in range(0, n-i-1):
        # Swap if the present element is greater than the
        # next element.
            if arr[j] > arr[j+1]:
                temp = arr[j]
                arr[j] = arr[j+1]
                arr[j+1] = temp 
    return arr

# main code
if __name__=='__main__':

    arr = [2, 1, 9, 3, 7, 5, 6, 4, 8, 0]
    print("Sorted array: ")
    print(bubble_sort(arr))

The output of the above program will be:

Sorted array: 
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]