Home »
Algorithms
Find the roots of a complex polynomial equation using Regula Falsi Method in C
In this article, we are going to learn how to find the roots of a complex polynomial equation using Regula Falsi Method?
Submitted by Sneha Dujaniya, on June 09, 2018
Regula Falsi method
About the method:
We often hear many children and even many adults complaining about the difficulty level that they face while solving complex polynomial equations. It is also difficult for many to follow the steps in a scientific calculator and find the roots of the equations.
Therefore, this is a program that would help engineering students and many shopkeepers, vendors to solve complex equations via the False Position method or the Regula Falsi method. It is also handy, easy and calculations need not be done.
Though this is an old method and not much used now it can be useful for those students who are willing to work on a complex project and on a difficult topic like this as they can create a better impression on their professors and fetch more marks. The method used is:
We start this procedure by locating two points x0 and x1 where the function has opposite signs. We now connect the two points f(x0) and f(x1) by a straight line and find where it cuts the x-axis. Let it cut the axis at x2. We find f(x2). If f(x2) and f(x0) are of opposite signs then we replace x1 by x2 and draw a straight line connecting f(x2) to f(x0) to find the new intersection point. If f(x2) and f(x0) are of the same sign then x0 is replaced by x2 and proceed as before. In both cases, the new interval of search is smaller than the initial interval and ultimately it is guaranteed to converge to the root.
We will now get an equation to find the successive approximations to the root:
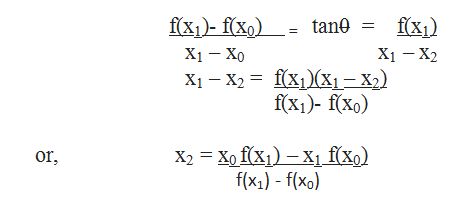
Problem:
To find the roots of the given polynomial equation using the Regula Falsi method. Here, we take the equation in the form of f(x) = ax2+ bx+c if the equation is a quadratic equation.
Example: f(x) = x2-25
In this method, we need to assume 2 numbers which might be the roots of the equation by equating the equation f(x) to zero {f(x) = 0}. If the actual roots do not lie between or are near to the assumed values, the program will not run. And if the actual roots lie between the assumed values then the program will give the approximate of exact answer.
Example/program:
#include <stdio.h>
#include <math.h>
#define ep 0.001
float poly(float ar[], int, float);
int main()
{
float a[10],y0,y1,y2,x0,x1,x2,s,r;
int i,n;
char flag;
printf("\t\t\t*****REGULA FALSI METHOD*****");
//enter 2 if it is quadratic eq.
printf ("\n\n Please enter the degree of polynomial equation: ");
scanf ("%d", &n);
if (n>1)
{
for (i=0;i<=n; i++)
{
printf ("Enter the coefficient of x to the power %d: ", i);
scanf ("%f", &a[i]);
}
do
{
//enter assumed values of roots
printf ("\n Enter the initial guesses of x0 and x1: ");
scanf ("%f %f",&x0,&x1);
y0=poly (a, n, x0);
y1=poly (a, n, x1);
} while (y0*y1>0);
printf ("\n x0 x1 x2 y0 y1 y2");
for (i=0; i<=100; i++)
{
s= (x0*y1)-(y0*x1);
r= y1-y0;
x2 = s/r;
y2 = poly (a, n, x2);
if (fabs (y2)<= ep)
{
flag ='T';
break;
}
printf("\n %f %f %f %f %f %f",x0,x1,x2,y0,y1,y2);
if ((y2*y0)<0)
{
x1=x2;
y1=y2;
}
else
{
x0=x2;
y0=y2;
}
}
if(flag=='T')
printf("\n\n Convergent solution= %f",x2);
else
printf("Does not converge in 100 iterations.");
}
else
{
printf("\n\tDegree not acceptable!");
}
return 0;
}
float poly(float ar[],int n,float x)
{
int i;
float p;
p=ar[n];
for(i=n;i>=1;i--)
{
p=ar[i-1]+(x*p);
}
return (p);
}
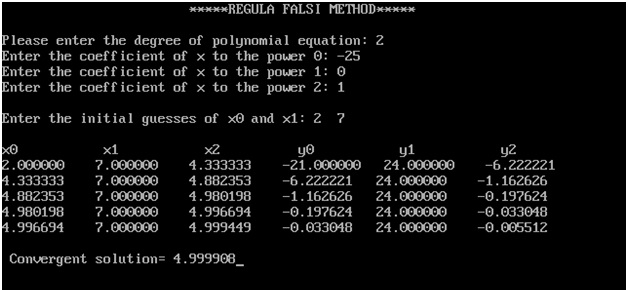
Output:
Advertisement
Advertisement