Home »
Algorithms
Huffman Coding (Algorithm, Example and Time complexity)
This article contains basic concept of Huffman coding with their algorithm, example of Huffman coding and time complexity of a Huffman coding is also prescribed in this article.
Submitted by Abhishek Kataria, on June 23, 2018
Huffman coding
- Huffman Algorithm was developed by David Huffman in 1951.
- This is a technique which is used in a data compression or it can be said that it is a coding technique which is used for encoding data.
- This technique is a mother of all data compression scheme.
- This idea is basically dependent upon the frequency, i.e. the frequency of the corresponding character which needs to be compressed, and by that frequency, only Huffman code will be generated.
- In case of Huffman coding, the most generated character will get the small code and least generated character will get the large code.
- Huffman tree is a specific method of representing each symbol.
- This technique produces a code in such a manner that no codeword is a prefix of some other code word. These codes are called as prefix code.
Algorithm for Huffman code
1. Input:-Number of message with frequency count.
2. Output: - Huffman merge tree.
3. Begin
4. Let Q be the priority queue,
5. Q= {initialize priority queue with frequencies of all symbol or message}
6. Repeat n-1 times
7. Create a new node Z
8. X=extract_min(Q)
9. Y=extract_min(Q)
10. Frequency(Z) =Frequency(X) +Frequency(y);
11. Insert (Z, Q)
12. End repeat
13. Return (extract_min(Q))
14. End.
Example:
Let obtain a set of Huffman code for the message (m1.....m7) with relative frequencies (q1.....q7) = (4,5,7,8,10,12,20). Let us draw the Huffman tree for the given set of codes.
Step 1) Arrange the data in ascending order in a table.
4,5,7,8,10,12,20
Step 2) Combine first two entries of a table and by this create a parent node.
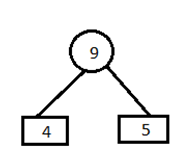
Step 3)
A) Remove the entries 4 and 5 from the table and inert 9 at its appropriate position. 7,8,9,10,12,20
Combine minimum value of table and create a parent node.
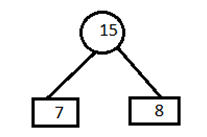
B) Now remove the entries 7 and 8 from the table and insert 15 at its appropriate position. 9,10,12,15,20
Combine minimum value of two blocks and create a parent node.
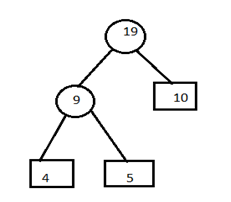
C) Remove the entries 9 and 10 from the table and insert 19 at its proper position. 12,15,19,20.
Combine minimum value of two blocks and create parent node.
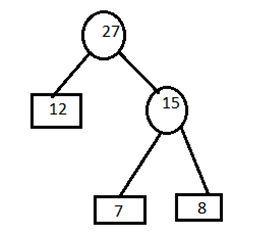
D) Remove the entries 15 and 12 from the table and insert 27 at its appropriate position. 19,20,27
Combine minimum value of two blocks and create parent node.
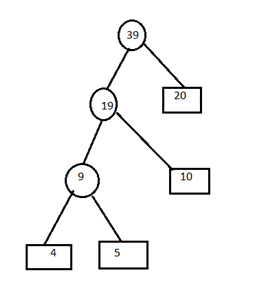
E) Remove the entries 19 and 20 from the table and insert 39 in the table. 27,39
Combine minimum value of two blocks and create parent node.
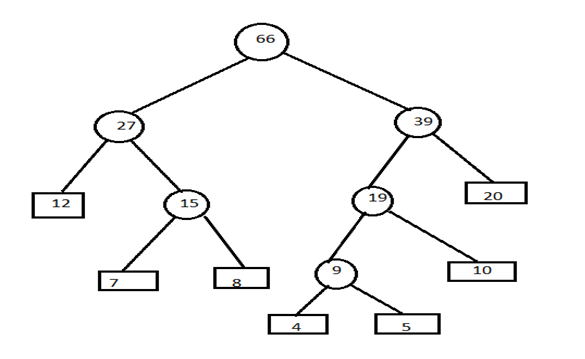
Step 4) Now assign left child as 0 and right child as 1 to encode the frequencies.
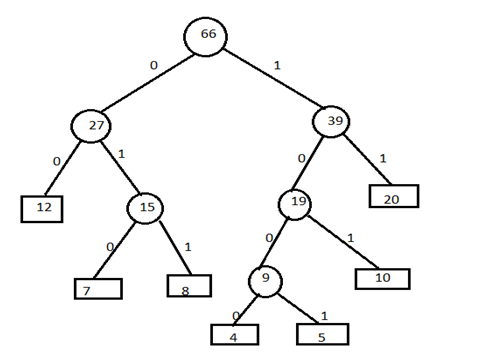
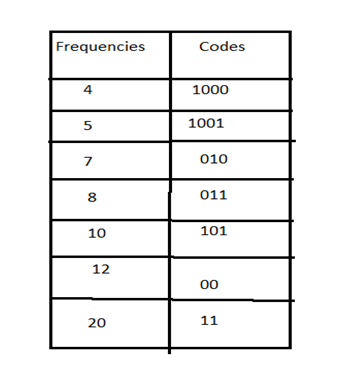
Now, codes for the given frequencies are given below:
Time complexity:
O(nlogn) is the overall time complexity. Where n is the number of characters.
Advertisement
Advertisement