Home » Algorithms

Implementation of Priority Scheduling (Pre-emptive) algorithm using C++

In this article, we are going to learn about priority scheduling algorithm (pre-emptive) and implementing this algorithm using C++ program.
Submitted by Aleesha Ali, on January 29, 2018

Pre-emptive: If a process of higher priority comes then first CPU will be assign to the Process with higher priority first.

Scheduling criteria tells us that any algorithm is how much efficient, the main criteria of scheduling are given below:

• CPU Utilization
• Throughput
• Arrival time
• Turnaround time
• Waiting time
• Completion time
• Burst time

*Ready Queue is a queue where all the processes wait to get CPU for its execution.

CPU Utilization: The amount of time CPU is busy.

Throughput: The number of process computed per unit time.

Arrival time: The time at which the process enters into ready queue.

Turn around time: The interval between the time of submission of a process to the time of completion.

Waiting time: The total amount of the time a process spends in ready queue.

Completion time: The time at which process completes its execution.

Burst time: The time needed by CPU to completes its execution.

Priority Scheduling Algorithm

In this algorithm priority is defined by manufacture of operating system, sometimes we assume minimum number has higher priority or vice a versa.

In my algorithm I use higher number has higher priority means process having higher priority will be schedule first.

C++ Program for Priority Algorithm

//Implementation of Priority(Preeemptive) Using C++
#include <iostream>
#include <algorithm>
#include <string.h>
using namespace std;

typedef struct proccess
{
	int at,bt,ct,ta,wt,btt,pr;
	string pro_id;
	/*
	artime = Arrival time,
	bt = Burst time,
	ct = Completion time,
	ta = Turn around time,
	wt = Waiting time
	*/

}schedule;

bool compare(schedule a,schedule b)
{
	return a.at<b.at;
	/* This schedule will always return TRUE
	if above condition comes*/
}

bool compare2(schedule a,schedule b)
{
	return a.pr>b.pr;
	/* This schedule will always return TRUE
	if above condition comes*/
}

int main()
{
	schedule pro[10];
	int n,i,j,pcom;

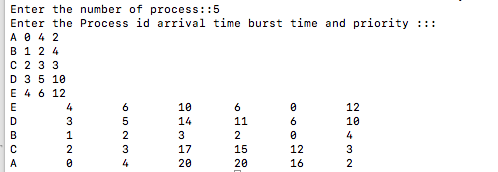
	cout<<"Enter the number of process::";
	cin>>n;
	cout<<"Enter the Process id arrival time burst time and priority :::";
	for(i=0;i<n;i++)
	{
		cin>>pro[i].pro_id;
		cin>>pro[i].at;
		cin>>pro[i].bt;
		pro[i].btt=pro[i].bt;
		cin>>pro[i].pr;
	}

	sort(pro,pro+n,compare);
	/*sort is a predefined funcion  defined in 
	algorithm.h header file, it will sort the 
	schedulees according to their arrival time*/

	i=0;
	pcom=0;
	while(pcom<n)
	{
		for(j=0;j<n;j++)
		{
			if(pro[j].at>i)
			break;
		}
		sort(pro,pro+j,compare2);
		if(j>0)
		{
			for(j=0;j<n;j++)
			{
				if(pro[j].bt!=0)
				break;
			}
			if(pro[j].at>i)
			i+=pro[j].at-i;
			pro[j].ct=i+1;
			pro[j].bt--;
		}
		
		i++;
		pcom=0;
		for(j=0;j<n;j++)
		{
			if(pro[j].bt==0)
			pcom++;
		}
	}

	for(i=0;i<n;i++)
	{
		pro[i].ta=pro[i].ct-pro[i].at;
		pro[i].wt=pro[i].ta-pro[i].btt;
		//before executing make it in one statement
		cout<<pro[i].pro_id<<"\t"<<pro[i].at<<"\t"<<pro[i].btt<<"\t"<<pro[i].ct<<"\t"<<pro[i].ta<<"\t"<<pro[i].wt<<"\t"<<pro[i].pr;
		cout<<endl;
	}

	return 0;
}

Output