Home »
Algorithms
4 Queen's problem and solution using backtracking algorithm
In this article, we are going to learn about the 4 Queen's problem and how it can be solved by using backtracking?
Submitted by Shivangi Jain, on June 29, 2018
4 - Queen's problem
In 4- queens problem, we have 4 queens to be placed on a 4*4 chessboard, satisfying the constraint that no two queens should be in the same row, same column, or in same diagonal.
The solution space according to the external constraints consists of 4 to the power 4, 4-tuples i.e., Si = {1, 2, 3, 4} and 1<= I <=4, whereas according to the internal constraints they consist of 4! solutions i.e., permutation of 4.
Solution of 4 – queen’s with the help of backtracking
We can solve 4-queens problem through backtracking by taking it as a bounding function .in use the criterion that if (x1, x2, ……., xi) is a path to a current E-node, then all the children nodes with parent-child labelings x (i+1) are such that (x1, x2, x3, ….., x(i+1)) represents a chessboard configuration in which no queens are attacking.
So we start with the root node as the only live node. This time this node becomes the E-node and the path is (). We generate the next child. Suppose we are generating the child in ascending order. Thus the node number 2 is generated and path is now 1 i.e., the queen 1 is placed in the first row and in the first column.
Now, node 2 becomes the next E-node or line node. Further, try the next node in the ascending nodes i.e., the node 3 which is having x2 = 2 means queen 2 is placed in the second column but by this the queen 1 and 2 are on the same diagonal, so node 3 becomes dead here so we backtrack it and try the next node which is possible.
Here, the x2 = 3 means the queen 2 is placed in the 3rd column. As it satisfies all the constraints so it becomes the next live node.
After this try for next node 9 having x3 = 2 which means the queen 3 placed in the 2nd column, but by this the 2 and 3 queen are on the same diagonal so it becomes dead. Now we try for next node 11 with x3 = 4, but again the queens 2 and 3 are on the same diagonal so it is also a dead node.
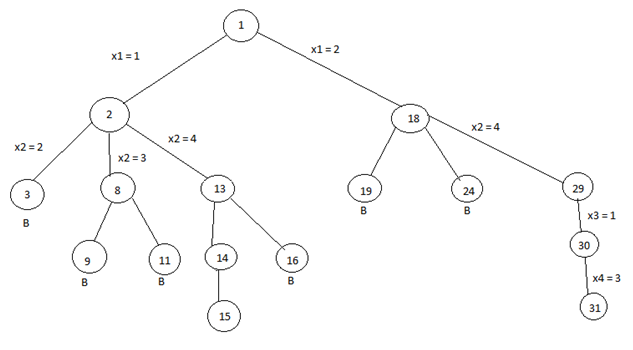
* The B denotes the dead node.
We try for all the possible positions for the queen 3 and if not any position satisfy all the constraints then backtrack to the previous live node.
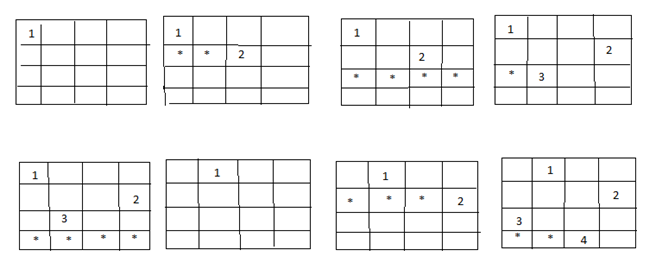
Now, the node13 become the new live node with x2 = 4, means queen 2 is placed in the 4th column. Move to the next node 14. It becomes the next live node with x3 = 2 means the queen 3 is placed in the 2nd column. Further, we move to the next node 15 with x4 = 3 as the live node. But this makes the queen 3 and 4 on the same diagonal resulting this node 15 is the dead node so we have to backtrack to the node 14 and then backtrack to the node 13 and try the other possible node 16 with x3 = 3 by this also we get the queens 2 and 3 on the same diagonal so the node is the dead node.
So we further backtrack to the node 2 but no other node is left to try so the node 2 is killed so we backtrack to the node 1 and try another sub-tree having x1 = 2 which means queen 1 is placed in the 2nd column.
Now again with the similar reason, nodes 19 and 24 are killed and so we try for the node 29 with x2 = 4 means the queen 2 is placed in the 4th column then we try for the node 30 with x3 = 1 as a live node and finally we proceed to next node 31 with x4 = 3 means the queen 4 is placed in 3rd column.
Here, all the constraints are satisfied, so the desired result for 4 queens is {2, 4, 1, 3}.
Advertisement
Advertisement