Home »
Algorithms
Algorithm for fractional knapsack problem
In this article, we are going to learn about fractional knapsack problem. Algorithm for fractional knapsack with its example is also prescribed in this article.
Submitted by Abhishek Kataria, on August 02, 2018
Knapsack problem
The knapsack problem or rucksack problem is a problem in combinative or integrative optimization. In this kind of problem, there are set of items are given with a weight and a value, determine the number of each item included in a collection so that the total weight is less than or equal to the given limit and the total value is as large as possible.
Fractional Knapsack problem
In fractional knapsack fractions of an item can be taken rather than having to make a binary choice for each of them. In this objective function is mathematically represented by:
Max 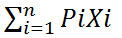
Where, Pi= profit and Xi = fraction.
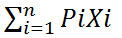
Where, Wi = weight of the corresponding and Xi= fraction.
In this, at last, the output should be an array of the fraction item that we have taken, and in this, we also have to take output that gives the maximum profit.
Algorithm for fractional knapsack
1. W and item have value Vi and weight Wi.
2. Rank item by value/weight ratio: Vi/Wi.
3. Thus : Vi/Wi= Vj/Wj for all i<=Wj.
4. Consider items in order of descending ratio.
5. Take as much of each item is possible.
6. Assume value and weight arrays are
sorted by Vi<=Wi fractional knapsack (V,w,W)
7. Load:=0
8. i:=1
9. while load<w and i<=n loop
10. if
11. wi <=W –loop then
12. take all of item i
13. else
14. take (W-load)/wi of item i
15. end if
16. Add weight of what was taken to load.
17. i:i+1
18. end loop
19. return loop
Example of fractional knapsack for the following instance by using greedy approach in which maximum value, M =25kg.
| S.no |
Weight |
Profit |
| 1 |
10 |
30 |
| 2 |
5 |
20 |
| 3 |
15 |
40 |
| 4 |
8 |
36 |
P=
W=
Now we will calculate the profit per unit capacity of knapsack: P/W
Now the fraction i.e. X
i.e. to calculate a total profit:
P = P1X1 + P2X2 + P3X3 + P4X4
= 30×1+20×1+40×2/15+36×1
= 91.33
Advertisement
Advertisement