Home »
Machine Learning/Artificial Intelligence
N-Queens Problem- A Type of Constraint Satisfactory Problem in AI
In this tutorial, we are going to study a famous Constraint Satisfactory Problem of Artificial Intelligence. We will study what the N-Queen problem is, what set of constraints it has and how the agent works while keeping all these constraints satisfied, and how the goal state is reached by the agent?
By Monika Sharma Last updated : April 12, 2023
N-Queens Problem
N-Queens problem is a well-known Constraint Satisfactory Problem of Artificial Intelligence. In this problem, we have an NxN square grid board and we have N queens which need to be placed on them.
Constraints
The queens should be placed on the board in such a way so that it satisfies the below-mentioned constraints:
- No row should contain more than one queen placed in it
- No column should contain more than one queen placed in it.
- Not more than one queen should be placed in the single diagonal.
- No row or column should be left without any queen placed in it.
On summing up all the constraints, we can conclude that each row and each column should contain exactly one queen in them, neither more nor less than that.
In this series of problems, mostly there are grids whose size is even in number, like 4, 6, 8 and so on. It should be noted that the minimum number of the grid that we can have in this problem is 4, not less than that.
N-Queens Problem Series
Here the 4-Queen problem and the 8-Queen problem are the most popular in the N-Queen problem series. There can exist many solutions for solving this problem, which mean that the solution to these problems is not unique. Yet, one of those solutions to both these types are given below:
1. 4-Queens Problem
In the 4-Queens problem, we have a 4x4 grid and we have 4 queens to place on it. The layout for the 4-Queens problem while satisfying all the constraints is as follows:
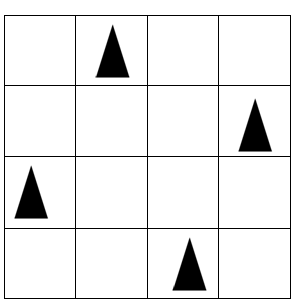
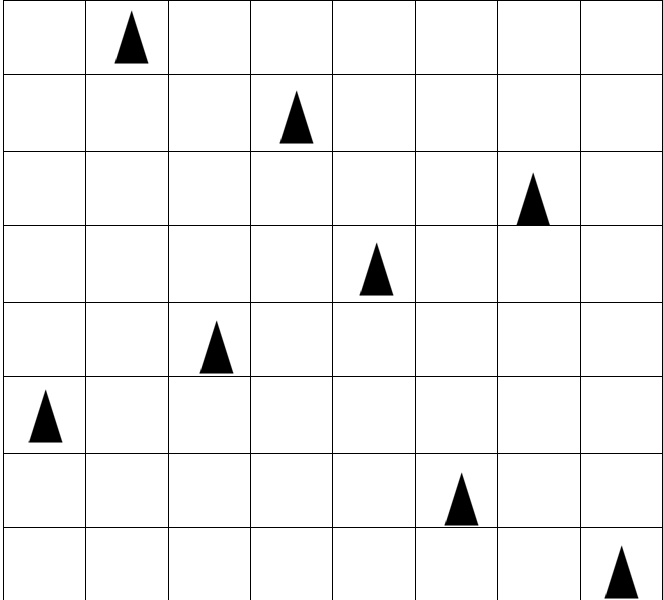
2. 8-Queens Problem
In the 8-Queens problem, we have an 8x8 grid and we have 8-queens to place on it. The layout for the 8-Queens problem while satisfying all the constraints is as follows:
Advertisement
Advertisement