Home » C programs » C advance programs

C program to solve Polynomial and Differential Equations

In this program, we will learn how to solve polynomial and differential equations using C programming language?
Submitted by Sneha Dujaniya, on July 31, 2018

1) Polynomial Evaluation

We all know what polynomial equations are and it is one of the common problems given to the beginners when they first start learning C. So, there is a simple program shown below which takes the use of functions in C language and solve the polynomial equation entered by the user provided they also enter the value of the unknown variable x.

For example, the polynomial equation that we use in our program is f(x) = 2x²+3x+1. Now, we ask the user for the value of x. Suppose, x = 2. After putting this value in f(x) = 2*2²+ 3*2+1, we get the answer as f(x) = 15.

This program exactly does the same calculation with the help of the fact that we can pass an entire array as our function parameter.

C program to solve polynomial equation

#include <stdio.h>
#include <conio.h>

float poly(float a[], int, float);

int main()
{
    float x, a[10], y1;
    int deg, i;

    printf("Enter the degree of polynomial equation: ");
    scanf("%d", &deg);

    printf("Ehter the value of x for which the equation is to be evaluated: ");
    scanf("%f", &x);

    for (i = 0; i <= deg; i++) {
        printf("Enter the coefficient of x to the power %d: ", i);
        scanf("%f", &a[i]);
    }

    y1 = poly(a, deg, x);

    printf("The value of polynomial equation for the value of x = %.2f is: %.2f", x, y1);

    return 0;
}

/* function for finding the value of polynomial at some value of x */
float poly(float a[], int deg, float x)
{
    float p;
    int i;

    p = a[deg];

    for (i = deg; i >= 1; i--) {
        p = (a[i - 1] + x * p);
    }

    return p;
}

Output

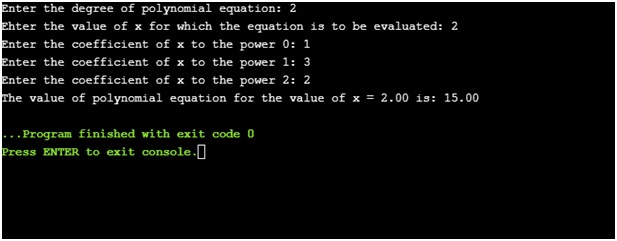
Dry run of the program:

When we call the poly() function, this is how it goes forward,

i	p = a[i-1] + x*p
2	p = a[2-1] + 2*a[2], since, p = a[deg] = a[2] p =3 + 2*2 = 7
1	p = a[1-1] + 2*7, since, the value of p is 7, now. p = 1 + 2*7 = 15

2) Differential solution

In this program, we find the value of the derivative of the polynomial equation using the same value of x. For example, we have the quadratic equation f(x) = 2x²+3x+1. The first derivative of this equation would be df(x) = 4x + 3. After the putting x = 2 in the derivative, we get df(x) = 4*2 +3 = 11.

For calculating the derivative, we call the deriv() function. Let’s see how the program runs.

C program to solve differential equation

#include <stdio.h>
#include <conio.h>
#include <math.h>

float poly(float a[], int, float);
float deriv(float a[], int, float);

int main()
{
    float x, a[10], y1, dy1;
    int deg, i;

    printf("Enter the degree of polynomial equation: ");
    scanf("%d", &deg);

    printf("Ehter the value of x for which the equation is to be evaluated: ");
    scanf("%f", &x);

    for (i = 0; i <= deg; i++) {
        printf("Enter the coefficient of x to the power %d: ", i);
        scanf("%f", &a[i]);
    }

    y1 = poly(a, deg, x);
    dy1 = deriv(a, deg, x);

    printf("The value of polynomial equation for the value of x = %.2f is: %.2f", x, y1);
    printf("\nThe value of the derivative of the polynomial equation at x = %.2f is: %.2f", x, dy1);

    return 0;
}

/* function for finding the value of polynomial at some value of x */

float poly(float a[], int deg, float x)
{
    float p;
    int i;

    p = a[deg];

    for (i = deg; i >= 1; i--) {
        p = (a[i - 1] + x * p);
    }

    return p;
}

/* function for finding the derivative at some value of x */
float deriv(float a[], int deg, float x)
{
    float d[10], pd = 0, ps;
    int i;

    for (i = 0; i <= deg; i++) {
        ps = pow(x, deg - (i + 1));
        d[i] = (deg - i) * a[deg - i] * ps;
        pd = pd + d[i];
    }

    return pd;
}

Output

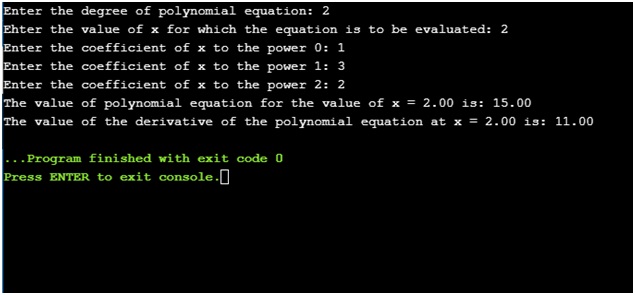
Dry run of the program:

When we call the deriv() function, this is how it goes forward,

i	ps	d[i]	pd
0	x1	2*2*x1 = 8	8
1	x0	1*3*x0 = 3	8+3 =11
2	x-1	0*1*x-1 =0	11+0 = 11

C Advance Programs »