Home » Data Structure

Asymptotic Notations

Learn: What are Asymptotic Notations? How they are used to express the time complexity of algorithm?
Submitted by Abhishek Jain, on July 27, 2017

Asymptotic notation employs the following notations to express the time complexity of algorithms. These are termed asymptotic notation since they are meaningful approximations of functions that represent the time or space complexity of a program.

The asymptotic notation is nothing but to assume the value of a function. In this notation the complexity is usually expressed in the form of a function f(n) , where 'n' is the input size for a given instance of the problem being solved.

The most commonly used asymptotic notations are:

1) Big O Notation

Big O is the formal method of expressing time complexity in terms of the upper bound value of an algorithms running time. It’s a measure of the longest amount of time it could possibly take for the algorithm to complete.

Definition: f(n)=O(g(n))

If there are two positive constants c and n₀ such that

|f(n)|<= c|g(n)| for all n >= n₀

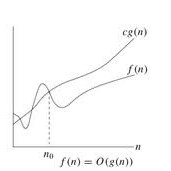
Based on Big O notation, the algorithms can be categorized as follows:

• Constant running time algorithms: Algorithms reporting O(1) time complexity.
• Logarithmic time algorithms: O(logn) time complexity is referred to as logarithmic.
• Linear time algorithms: The time complexities of O(n) are called lineartime complexities.
• Polynomial time algorithms: In general , time complexities of the type O(n^k) are called polynomial time complexities.
• Exponential time algorithms: Time complexities such as O(2ⁿ), O(3ⁿ), in general O(kⁿ) are called as exponential time complexities.

Some of the commonly occurring time complexities in their ascending orders of magnitude are listed below:

O(1) <= O(log n) <= O(n) <= O(n.log n) <= O(n2) <= O(n3) <= O(2n)

Example:

f(n)	g(n)
1) 16n3+78n2+12n	n3	f(n)=O(n3)
2) 34n – 90	N	f(n)=O(n)
3) 56	1	f(n)=O(1)

Here, g(n) is the upper bound of the function f(n).

2) Big Omega(Ω) Notation

The asymptotic notation used to denote space or time complexity in terms of lower bound value is called as Big Omega notation.

Definition: f(n)= Ω(g(n))

If there are two positive constants c and n₀ such that

|f(n)|>= c|g(n)| for all n >= n₀

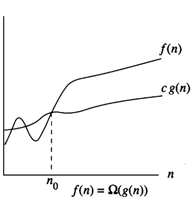
Example:

f(n)	g(n)
1) 16n3+8n2+2	n3	f(n)=Ω(n3)
2) 24n + 9	N	f(n)= Ω (n)

Here, g(n) is the lower bound of the function f(n).

3) Big Theta(θ) Notation

The asymptotic notation used to denote space or time complexity in terms of tight bound value is called as Big Theta (θ) Notation.These requires both Big O and Omega (Ω), so that’s why it’s referred to as a tight bound (it must be both the upper and lower bound).

Definition: f(n)=θ (g(n))

If there are two positive constants c_1,c² and n₀ such that

c₁|g(n)| <= |f(n)|<= c₂|g(n)| for all n >= n₀

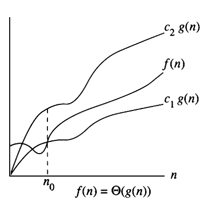
Example:

f(n)	g(n)
1) 28n + 9	N	f(n)= θ (n) since f(n)> 28n and f(n) <= 37n for n >=1
2) 16n2+30n-90	n2	f(n)= θ (n2)
3) 7.2n + 30n	2n	f(n)= θ (2n)

From the definition it implies that the function g(n) is both an upper bound and a lower bound for the function f(n) for all values of n, n>=n₀. This means that f(n) is such that , f(n)= O(g(n)) and f(n)= Ω(g(n)).

Reference: http://www.personal.kent.edu/~rmuhamma/Algorithms/MyAlgorithms/intro.htm