Home » Data Structure

Construct a binary search tree from a sorted 1-D array

In this article, we are going to see how to create a binary search tree from a sorted array?
Submitted by Radib Kar, on October 11, 2020

Prerequisite: Create a BST from the sorted linked list

In this article, we are going to see how we can create a height-balanced binary Search tree from a given sorted 1-D array?  Pay attention to the word "height-balanced" as it plays a huge role. We can create a binary search tree with the list by just creating a skew tree from the array elements, where we will just put the list nodes as a right child only. For example,

Let's say the sorted array is:

Then the skew tree that can be created from this would be:

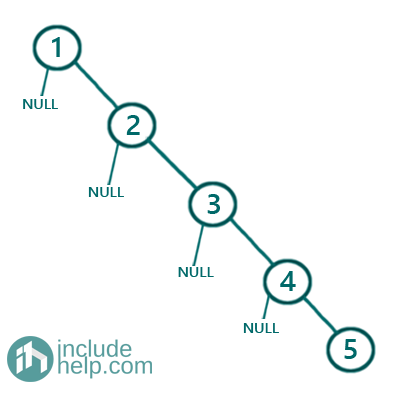
Though this is a Binary Search tree, it's not what we are expecting as it's not height-balanced. For a height-balanced tree, the difference between the left & right subtree will be maximum 1. So below is the approach to create a height-balanced binary search tree from a sorted array.

1. Find the middle of the sorted list, which is array [first index+ (last index-first index+1)/2]
2. The middle node is the root, left part of the middle node is the left subtree & right part is the right subtree
3. Recursively construct left subtree & right subtree.

To illustrate the algorithm visually, below is the step by step pictorial representation:

Firstly the array is,

So we find the middle and create a root node from the middle element of the sorted array.

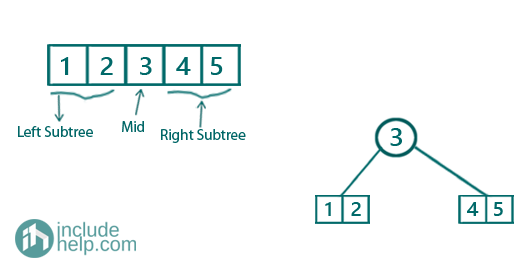
Now we recursively create the left subtree,

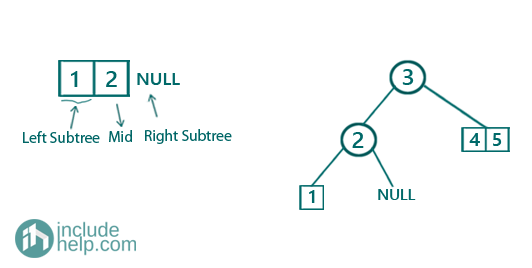
Now the array [1] a single element and that would return a leaf node in the tree whereas NULL will be NULL in the tree as well. So after constructing the left subtree the semi-constructed BST would be:

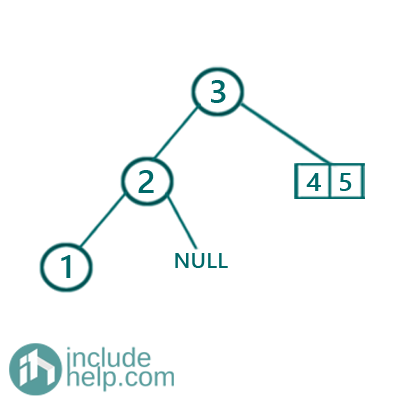
Now, creating the right subtree similarly,

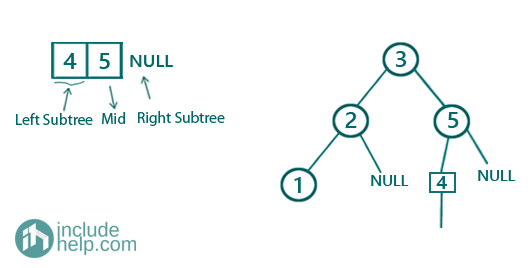
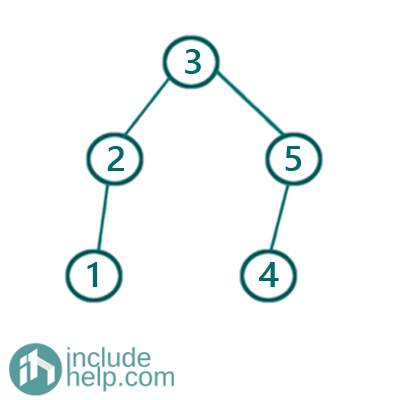
Then finally the BST would be:

N.B: this a height-balanced BST, but not only one. You can create another BST out of this which is still height-balanced and that would be like below:

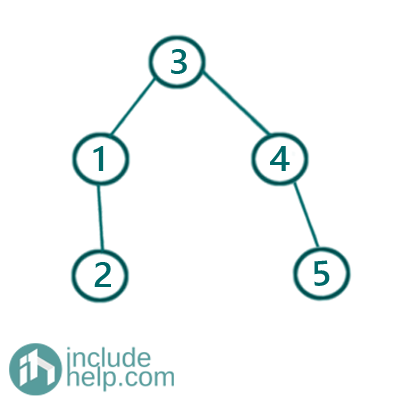
It's due to the middle element we are picking up. In case of an odd-sized array, there is no problem, but in case of an even-sized array there is two middle elements and based on which one we pick, there can be many such combinations. In our implementation, we have always chosen the second middle element in case of an even-sized array as our middle element to create the root.

Below is the C++ implementation,

#include <bits/stdc++.h>
using namespace std;

// tree node is defined
class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int data)
    {
        val = data;
        left = NULL;
        right = NULL;
    }
};

void inorder(TreeNode* root)
{

    if (!root)
        return;
    inorder(root->left);
    cout << root->val << " ";
    inorder(root->right);
}
TreeNode* sortedArrayToBST(vector<int> arr, int start, int end)
{
    //base cases
    //empty array
    if (start > end)
        return NULL;
    //single element array
    if (start == end)
        return new TreeNode(arr[start]);

    //find the middle of the array
    int mid = start + (end - start + 1) / 2;
    TreeNode* root = new TreeNode(arr[mid]);
    //recursively create left subtree 
    //from the left part[start,mid-1]
    root->left = sortedArrayToBST(arr, start, mid - 1);
    //recursively create left subtree from 
    //the right part[mid+1, end]
    root->right = sortedArrayToBST(arr, mid + 1, end);

    return root;
}

int main()
{
    int n;
    
    cout << "Enter array size\n";
    cin >> n;
    
    vector<int> arr(n);
    
    cout << "Enter the elements in sorted order(increasing)\n";
    for (int i = 0; i < n; i++)
        cin >> arr[i];
    
    cout << "Creating self-balancing BST from the sorted list\n";
    
    TreeNode* root = sortedArrayToBST(arr, 0, arr.size() - 1);
    
    cout << "height balanced BST created ...\n";
    cout << "root of the BST created is: " << root->val << endl;
    cout << "Inorder traversal of the BST\n";
    
    inorder(root);
    
    cout << endl;

    return 0;
}

Output:

Enter array size
5
Enter the elements in sorted order(increasing)
1 2 3 4 5
Creating self-balancing BST from the sorted list
height balanced BST created ...
root of the BST created is: 3
Inorder traversal of the BST
1 2 3 4 5