Home »
Data Structure
Construct BST from Given Preorder Traversal
In this article, we are going to see how to construct a BST from its preorder traversal?
Submitted by Radib Kar, on September 19, 2020
Prerequisite:
Earlier while discussing the construction of a binary tree, we found that to construct a binary tree, we need at least two traversals out of which one is inorder and another one can be anyone from preorder, postorder or level order. The reason was one traversal alone was not enough to distinguish the boundary between the subtrees.
But here, we are found that we are going to construct a Binary Search tree from the given preorder traversal. The first thing is it possible at all? In case a binary tree it was not possible, so why it's possible for a Binary search tree. Let's take an example to discuss that.
Let's the preorder traversal be: [8, 5, 1, 7, 10, 12]
Since it's a preorder traversal we know that the first item from the preorder traversal will be the root. Rest part is the subtree. Now, in case of a binary tree, we were not able to distinguish between the left & right subtree. But BST has the property that all nodes in the left subtrees will be less than the root value and all the nodes in the right subtree would be greater than the node. And we know that in preorder traversal, First, we traverse the root, then we traverse the left subtree and finally the right subtree. Now, we can distinguish b/w the subtrees using the BST property. Because all the nodes after the root in the traversal having values less than the node will fall in the left subtree and rest one will fall in the right subtree. Then we will construct the subtrees recursively.
Below is the step by step construction for the above preorder traversal.
Firstly, preorder[0] is the root and left subtree part would be the elements less than 8(preorder[0]), [5, 1, 7] and the right subtree would be [10, 12]
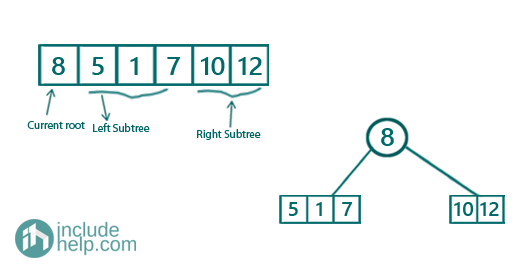
Now recursively constructing the left subtree,
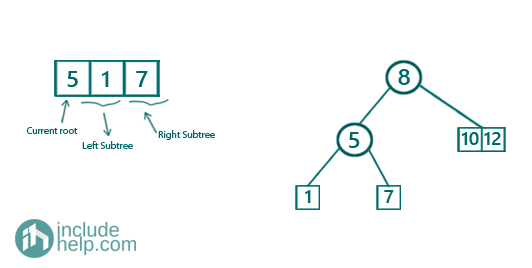
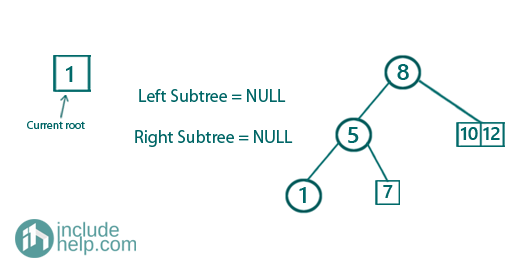
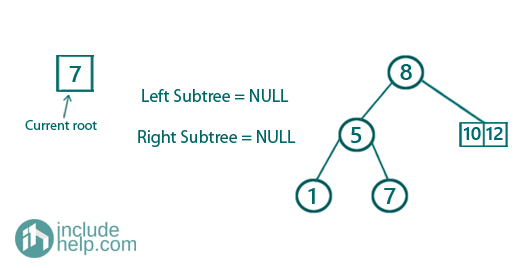
Constructing the right subtree,
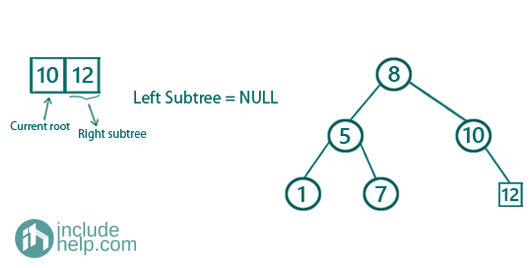
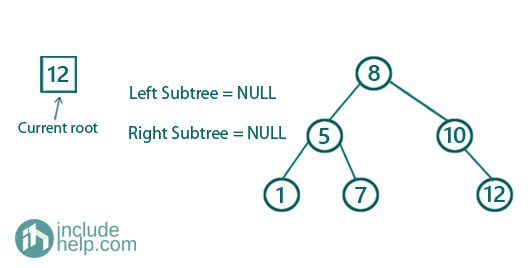
So the final constructed BST is:

Below is the cpp implementation of the above:
#include <bits/stdc++.h>
using namespace std;
// tree node is defined
class TreeNode {
public:
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int data)
{
val = data;
left = NULL;
right = NULL;
}
};
//inorder traversal for tree
void inorder(TreeNode* root)
{
if (!root)
return;
inorder(root->left);
cout << root->val << " ";
inorder(root->right);
}
//to find next greater element of the root in the range in O(logn) time
//this will find the starting index of the right subtree if exists
int FindNextGreater(vector<int>& preorder, int l, int r, int key)
{
int index = r + 1;
while (l <= r) {
int mid = l + (r - l) / 2;
if (preorder[mid] > key) {
index = mid;
r = mid - 1;
}
else {
l = mid + 1;
}
}
return index;
}
//recursively Constructing the BST
TreeNode* bstFromPreorderRecur(vector<int>& preorder, int l, int r)
{
//base case for returning NULL
if (l > r)
return NULL;
//base case for leaf nodes
if (l == r) {
return new TreeNode(preorder[l]);
}
//building the tree
TreeNode* root = new TreeNode(preorder[l]);
//starting index of right subtree
int m = FindNextGreater(preorder, l + 1, r, preorder[l]);
//building the left subtree recursively
root->left = bstFromPreorderRecur(preorder, l + 1, m - 1);
//building the right subtree recursively
root->right = bstFromPreorderRecur(preorder, m, r);
return root;
}
//constructing the BST
TreeNode* bstFromPreorder(vector<int>& preorder)
{
return bstFromPreorderRecur(preorder, 0, preorder.size() - 1);
}
//main function
int main()
{
vector<int> preorder{ 8, 5, 1, 7, 10, 12 };
cout << "Constructing the BST from its preorder traversal\n";
TreeNode* root = bstFromPreorder(preorder);
cout << "Tree constructed\n";
cout << "Inorder traversal of the constructed BST is:\n";
inorder(root);
cout << endl;
return 0;
}
Output:
Constructing the BST from its preorder traversal
Tree constructed
Inorder traversal of the constructed BST is:
1 5 7 8 10 12
Another way to build the binary search tree from the preorder traversal is to insert the elements one by one as we have shown in the insertion. Below is the implementation of this approach using the same insertion function discussed in my article on insertion in a Binary Search Tree.
#include <bits/stdc++.h>
using namespace std;
// tree node is defined
class TreeNode {
public:
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int data)
{
val = data;
left = NULL;
right = NULL;
}
};
//inorder traversal for tree
void inorder(TreeNode* root)
{
if (!root)
return;
inorder(root->left);
cout << root->val << " ";
inorder(root->right);
}
TreeNode* insert(TreeNode* root, int Key)
{ //base case
// if root is NULL
if (!root)
return new TreeNode(Key); //this is the new root
//if root value is more than the Key,
//then we need to insert in the left subtree only
if (root->val > Key)
//recursively insert in the left subtree
root->left = insert(root->left, Key);
//if root value is less than the Key,
//then we need to insert in the right subtree only
else if (root->val < Key)
//recursively insert in the right subtree
root->right = insert(root->right, Key);
return root;
}
TreeNode* bstFromPreorder(vector<int>& preorder)
{
int n = preorder.size();
if (n == 0)
return NULL;
//initially root is NULL
TreeNode* root = NULL;
//insert each element one by one
for (auto v : preorder) {
root = insert(root, v);
}
return root;
}
//main function
int main()
{
vector<int> preorder{ 8, 5, 1, 7, 10, 12 };
cout << "Constructing the BST from its preorder traversal\n";
TreeNode* root = bstFromPreorder(preorder);
cout << "Tree constructed\n";
cout << "Inorder traversal of the constructed BST is:\n";
inorder(root);
cout << endl;
return 0;
}
Output:
Constructing the BST from its preorder traversal
Tree constructed
Inorder traversal of the constructed BST is:
1 5 7 8 10 12
I am not doing the dry run here as we have already covered this part in our article on insertion in a Binary Search Tree. You can do the dry run yourself by taking each of the element one by one and inserting them into the binary search tree.
Advertisement
Advertisement