Home » Data Structure

Aggressive Cows (On Binary Search)

Here, we are discussing problem named Aggressive Cows based on Binary and its solution.
Submitted by Indrajeet Das, on October 23, 2018

A farmer has built a long barn with N stalls. The stalls are placed in a straight manner at positions from x1, x2, ...xN. But his cows (C) are aggressive and don’t want to be near other cows. To prevent cows from hurting each other, he wants to place them in such a way so that the minimum distance between them is as large as possible. What is the largest minimum distance?

Constraints:

    N: 2<=N<=100,000
    C: 2<=C<=N
    Xi: 0<=Xi<=1,000,000,000

Input:

    Line1: Two integers N and C
    Next N lines: An integer for Xi stall's position

Example:

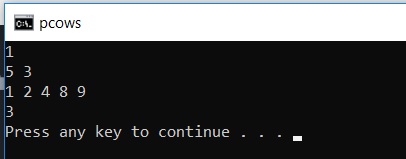
    Input: 
    5 3
    1 2 4 8 9

    Output:
    3

Explanation:

If the cows are placed at 1,4 and 9, it will result in minimum distance from 3.

SOLUTION AND CODE

Since the range of xi is from 0 to 10^9, one can say that the minimum distance between the cows will lie between the range. The minimum distance between 2 stalls can be 0 (lower bound) and maximum distance is 10^9 (upper bound). So, one can check for each value from lower bound to upper bound.

Let's say for k minimum distance, we can check if it is possible to place cows in the stall. In case, you have reached the last stall but didn’t have placed all cows, then it is not possible else it is possible.

A point to note is that if, for a k, it is possible to place the cows. Then all the values less than k will be true. Also, if k is false, then all the values greater than k will be false. We can say it is creating a monotonic function and we have to check for the transition from true to false and return that value.

It can be quickly and easily done with Binary Search from the range of 0 to 10^9.

CODE

#include <bits/stdc++.h>
using namespace std;

int N,C;

int check(int num,int stalls[])
{
	int cows=1,pos=stalls[0];
	for (int i=1; i<N; i++)
	{
		if (stalls[i]-pos>=num)
		{
			pos=stalls[i];
			cows++;
			if (cows==C)
				return 1;
		}
	}
	return 0;
}

int binarySearch(int stalls[])
{
	int start=0,end=stalls[N-1],max=-1;
	while (end>start)
	{
		int mid=(start+end)/2;
		if (check(mid,stalls)==1)
		{
			if (mid>max)
				max=mid;
			start=mid+1;
		}
		else
			end=mid;
	}
	return max;
}

int main()
{
	int t;
	cin>>t;

	while (t--)
	{
		cin>>N>>C;
		
		int stalls[N];
		
		for (int i=0; i<N; i++)
			cin>>stalls[i];
		
		sort(stalls,stalls+N);
		
		int k=binarySearch(stalls);
		
		cout<<k;
	}
	return 0;
}

Output