Home » Data Structure

Hamiltonian Cycle in Data Structure

In this article, we learn about the Hamiltonian cycle and how it can we solved with the help of backtracking?
Submitted by Shivangi Jain, on July 21, 2018

Hamiltonian Cycle

A Hamiltonian graph is the directed or undirected graph containing a Hamiltonian cycle. The Hamiltonian cycle is the cycle that traverses all the vertices of the given graph G exactly once and then ends at the starting vertex.

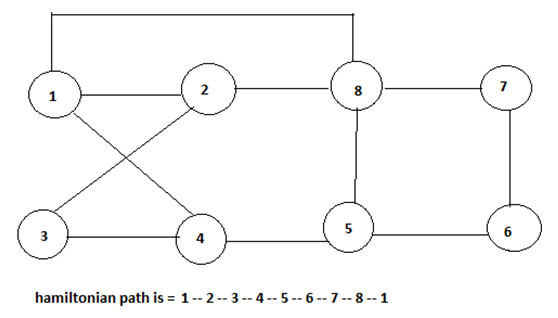
The input for the Hamiltonian graph problem can be the directed or undirected graph. The Hamiltonian problem involves checking if the Hamiltonian cycle is present in a graph G or not. The following graph illustrates the presence of the Hamiltonian cycle in a graph G.

While generating the state space tree following bounding functions are to be considered, which are as follows:

1. The i^th vertex in the path must be adjacent to the (i-1)^th vertex in any path.
2. The starting vertex and the (n-1)^th vertex should be adjacent.
3. The ith vertex cannot be one of the first (i-1)^th vertex in the path.

Algorithm:

    Algorithm Hamiltonian (k)
    1.	{
    2.	Repeat
    3.	{
    4.	Next value (k);
    5.	If (x[k] == 0) then return;
    6.	If ( x[k] == n) then write x[1:n];
    7.	Else Hamiltonian (k+1)
    8.	}
    9.	Until (false);

    Algorithm Next value (k)
    1.	{
    2.	Repeat
    3.	{
    4.	X [k] = (x[k] + 1 mod (n+1));
    5.	If (x[k] == 0) then return;
    6.	If (G (x[k-1]), x[k] =! 0) then
    7.	{
    8.	For j=1 to k-1
    9.	Do if ( x[ j ] == x[ k ]) then break;
    10.	If ( j == k) true
    11.	If ( k<n) or ( k = n ) and  G ( x[ n ], x[1] != 0)
    12.	}
    13.	Then return;
    14.	}
    15.	Until (false);
    16.	}
    17.	}

This algorithm uses the recursive formulated of backtracking to find all the Hamiltonian cycles of a graph. The graph is stored as an adjacency matrix G [1: n, 1: n].

In the next value k, x [1: k-1] is a path with k-1 distinct vertices. if x[k] == 0 then no vertex has to be yet been assign to x[k]. After execution x[k] is assigned to the next highest numbered vertex which does not already appear in the path x [1: k-1] and is connected by an edge to x [k – 1] otherwise x[k] == 0.

If k == n, (here n is the number of vertices) then in addition x[n] is connected to x [1].